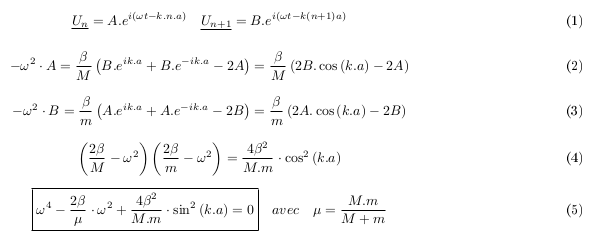Inscription / Connexion Nouveau Sujet
Vibrations de réseaux
Bonjour,
J'ai besoin de conseils pour résoudre un problème de mécanique.
Voici donc la première question:
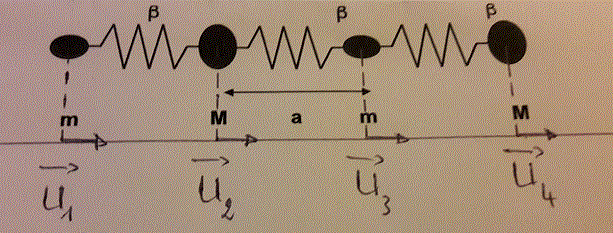
1°/ Calculer les fréquences propres de la chaîne infinie dont la composition est indiquée sur l'image.
Pour y répondre j'ai procédé de la manière suivante:
U1= déplacement de la première masse m
U2= déplacement de la première masse M et F2 la force qu'elle subit
U3= déplacement de la deuxième masse m et F3 la force qu'elle subit
U4= déplacement de la deuxième masse M
Est-ce que je suis sur la bonne voie?
Merci d'avance pour toutes vos suggestions
Bonjour
Pas de faute de signe a priori.
Juste une inattention dans la recopie de l'indice 3 dans l'expression de F2 :
Juste une question à 100 sous.
Ne doit-on pas introduire les longueurs à vide des ressorts (Lo) dans les relations ?

Ne doit-on pas introduire les longueurs à vide des ressorts (Lo) dans les relations ?
Les ressorts sont supposés parfaits. Les forces exercées par les ressorts dépendent de leurs allongements, pas de leurs longueurs !
S'il s'agit par la suite d'étudier la propagation d'une perturbation longitudinale le long des ressorts, la distance " a " va intervenir...
Les ressorts sont supposés parfaits. Les forces exercées par les ressorts dépendent de leurs allongements, pas de leurs longueurs !
Oui, cela j'avais bien compris.
Il n'empêche que ressort parfait ne présuppose pas de longueur au repos nulle.
... mais c'est vrai aussi que les Lo se simplifient dans les calculs.
Et donc par exemple la force exercée par le ressort de gauche sur la masse M est
F = k.(u2 - u1 - Lo)
et la force exercée par le ressort à droite de M de gauche sur la masse M est :
F' = k.(u3-u2-Lo)
Et donc F2 = F' - F
F2 = k.(u3-u2-Lo) - k.(u2 - u1 - Lo)
F2 = k.(u1 + u3-2.u2)
Et donc pas de soucis.

Bonjour Fina21
Je crois que, pour la suite, tu auras intérêt à écrire tes deux équations différentielles sous cette forme :
Ainsi, les atomes de rangs n, n+2, n+4 ... sont de masse M, les atomes de rang n+1, n+3, n+5... sont de masse m.
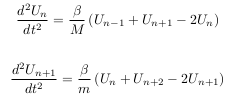
Bonsoir Fina21
Je me pose quelques questions sur ton énoncé. Dans le cas d'un nombre fini d'oscillateurs couplés, il existe un nombre fini de fréquences propres ; on peut donc demander de " calculer les fréquences propres".
Cependant, si la chaîne d'oscillateurs couplés est infinie comme précisé dans l'énoncé, on peut seulement montrer que la fréquence d'oscillation peut prendre une valeur quelconque à l'intérieur de deux domaines de fréquences disjoints, un domaine appartenant aux fréquences de l'acoustique, un domaine appartenant au domaine de l'optique...
Puisque je ne vais pas avoir accès pendant une semaine à mon éditeur d'équations, je te poste la modélisation qui se fait le plus souvent sur l'étude d'un cristal diatomique. Je n'ai pas l'énoncé précis, j'espère que cela pourra t'aider quand même. La méthode consiste à étudier la possibilité d'une propagation d'une perturbation sinusoïdale sous forme d'onde plane de pulsation  et de vecteur d'onde de norme k=2
et de vecteur d'onde de norme k=2 /
/ , la phase de l'onde étant ainsi (
, la phase de l'onde étant ainsi ( .t-k.x) avec x : abscisse d'équilibre d'un atome ou ion. On fait l'hypothèse que tous les atomes (ou ions) vibrent à la même pulsation
.t-k.x) avec x : abscisse d'équilibre d'un atome ou ion. On fait l'hypothèse que tous les atomes (ou ions) vibrent à la même pulsation  , l'amplitude de vibration des atomes de masse M est A, l'amplitude de vibration des atomes (ou ions) de masse m est B. Les élongations complexes des masses n et (n+1) sont ainsi : formule (1).
, l'amplitude de vibration des atomes de masse M est A, l'amplitude de vibration des atomes (ou ions) de masse m est B. Les élongations complexes des masses n et (n+1) sont ainsi : formule (1).
En reportant dans le système précisé dans mon message du 30-01-17 à 14:48 et en divisant tous les termes par exp[i( .t-k.n.a)], on obtient les formules (2) et (3).
.t-k.n.a)], on obtient les formules (2) et (3).
En éliminant A et B entre ces deux équations, on obtient la formule (4) qui peut se simplifier en (5).
Cette relation entre  et k est appelée relation de dispersion. A partir de là, plusieurs études sont possibles... Sachant que le carré du sinus est compris entre 0 et 1, on peut assez facilement démontrer les affirmations de mon message du 31-01-17 à 18:42. La suite dépend de l'énoncé...
et k est appelée relation de dispersion. A partir de là, plusieurs études sont possibles... Sachant que le carré du sinus est compris entre 0 et 1, on peut assez facilement démontrer les affirmations de mon message du 31-01-17 à 18:42. La suite dépend de l'énoncé...
Remarque : le serveur Latex du forum étant en panne, les formules postées, élaborées sous LaTex , sont ensuite converties en image de format png, ce qui dégrade un peu la qualité...