Inscription / Connexion Nouveau Sujet
Vibrations d'un pendule
Bonjour,
J'aurais besoin d'aide pour terminer cet exercice.
J'abrège un peu l'énoncé mais l'essentiel y est présent.
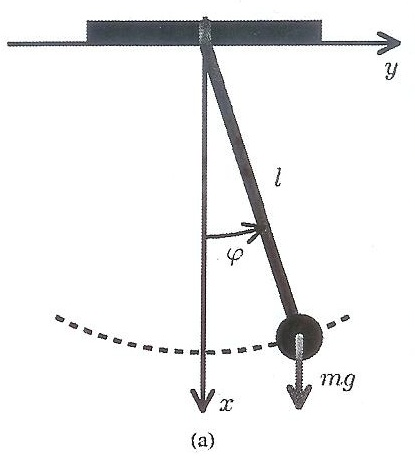
Considérez le pendule mathématique plan (exemple du pendule de Foucault : une balle de 28kg suspendue au bout d'une corde en acier de 1,5mm de diamètre et de longueur l = 67m).
1) Nombre de degrés de liberté, positions d'équilibres, choix des coordonnées. OK
2) Equation différentielle sans frottements ? OK
3) Avec force de frottements ? OK
4) Types de vibrations ? OK
5) Simplification à faible amplitude ?
On demande bien la simplification de l'équation sans frottements ? Si oui, OK.
6) Pulsation propre et période de vibration ?
OK sans frottements.
7) Solution générale ? Nombre de constantes d'intégration ?
OK sans frottements.
8) Solution particulière pour les conditions initiales (figure a) : {y(0) = 0 et dx/dt = vo} ?
y(0) est bien l'angle de départ qui vaut alors Pi/2 ? Et vo la vitesse de départ ?
9) On agit sur la masse m de façon périodique avec une force harmonique F tangente à la trajectoire de m et dont la composante tangentielle est Ft = f0 cos  t.
t.
Toujours dans l'approximation de petites amplitudes, obtenez l'équation différentielle.
Celle-ci me pose un souci.
10) Solution générale ? Simplification en régime stationnaire (t
 ) ?
) ?
Merci d'avance.
J'ai oublié de mettre l'image permettant de mieux comprendre la question 8 à propos du y, et je ne trouve pas comment éditer mon post.
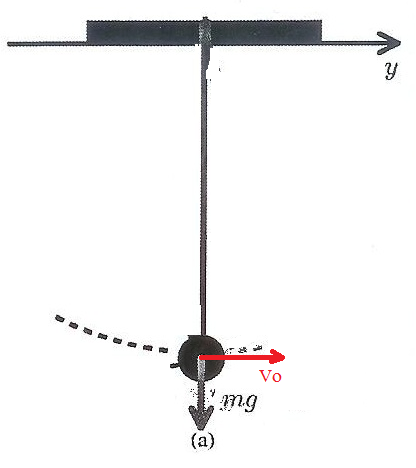
8)
y(0) = 0 signifie que la masse oscillante est à la verticale du point d'attache de la corde.
Donc la corde est, en cette position, confondue avec l'axe des x du repère (Phi = 0)
Et on a une vitesse Vo comme indiqué sur le dessin.
-----
9)
Avec ou sans frottement ???
Si sans frottement :
[- mg.sin(phi) + fo.cos(wt)]*L = m.L² * d²phi/dt²
Et si Phi reste petit, on peut remplacer sin(phi) par Phi et alors :
[- mg.phi + fo.cos(wt)]*L = m.L² * d²phi/dt²
m.L * d²phi/dt² + mg.Phi = fo.cos(wt)
d²phi/dt² + (g/L).Phi = (fo/(mL)).cos(wt)
---
Si frottement, alors ajouter la force de frottement (de quel type ?) ...
Sauf distraction. 
Merci pour la réponse, les forces de frottement sont du type -
 .
.
Pour la question 5, peut-on simplifier l'équation avec frottement pour obtenir la pulsation propre et la période de vibration ? Ça me semblait plus simple sans frottements mais ce n'est pas clairement indiqué dans l'énoncé...
Pour ma part, je pense qu'on peut négliger les frottements à basse amplitude.
Pour la question 10, il faut donc obtenir une solution particulière et une solution homogène ?
3)
[- mg.sin(phi) - Lambda * L * dphi/dt]*L = m.L² * d²phi/dt²
- mg.sin(phi) - Lambda * L * dphi/dt = m.L * d²phi/dt²
d²phi/dt² + (Lambda/m) * dphi/dt + (g/L).sin(phi) = 0
-----
6) (avec frottement)
Si faible amplitude, on peut assimiler sin(phi) à phi --->
d²phi/dt² + (Lambda/m) * dphi/dt + (g/L).phi = 0
p² + (Lambda/m).p + (g/L) = 0
p = [-(Lambda/m) +/- Racine((Lambda/m)² - 4g/L)]/2
Avec (frottement faible) : (Lambda/m)² - 4g/L < 0 --->
p = [-(Lambda/m) +/- i.Racine(4g/L - (Lambda/m)²)]/2
wo = [Racine(4g/L - (Lambda/m)²)]/2
wo = Racine[g/L - (Lambda²/(2m²)]
To = 2Pi/wo = ...
-----
7)
Phi(t) = e^(-(Lambda/(2m)).t) * [A . cos(Racine(g/L - (Lambda²/(2m²)).t) + B.sin(Racine(g/L - (Lambda²/(2m²)).t)].
-----
8)
Phi(t) = e^(-(Lambda/(2m)).t) * [A . cos(Racine(g/L - (Lambda²/(2m²)).t) + B.sin(Racine(g/L - (Lambda²/(2m²)).t)].
avec les conditions initiales : Phi(0) = 0 et (dphi/dt)(0) = Vo/L
On peut donc trouver les valeurs de A et de B ...
-----
Sauf distraction (pas vérifié). 
Merci pour la réponse.
Mais je me suis trompé et les forces de frottement sont du type - d
d /dt.
/dt.
Donc dans l'équation, on a donc : d² /dt² +
/dt² +  /ml d/dt + g/l
/ml d/dt + g/l  ?
?


