Inscription / Connexion Nouveau Sujet
Vibration tour
Bonjour,
je suis bloqué face à une question de l'exercice suivant :
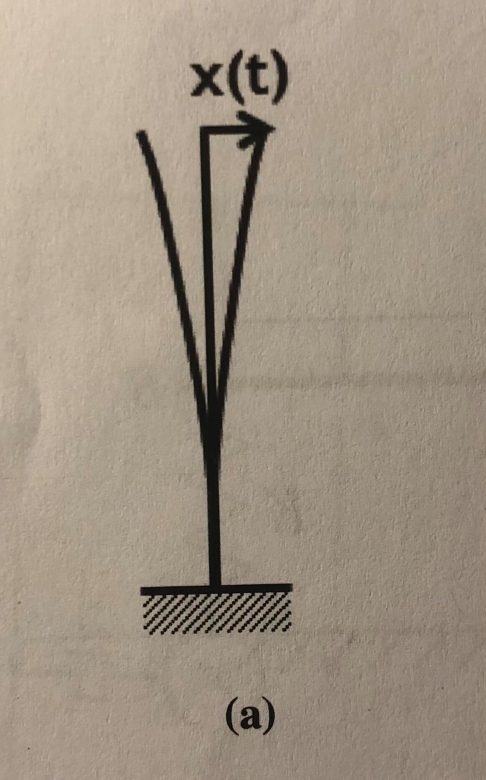
On s'intéresse aux vibrations latérales d'une tour (figure a) grâce à un système à 1 ddl "masse-ressort-amortisseur" (partie gauche de figure b). Généralement, en haut des tours, les vibrations sont si importantes qu'elles gênent les habitants. C'est pourquoi on décide d'installer une masse additionnelle à l'étage supérieur de la tour (partie droite de figure b). Cette masse est si importante qu'elle ne bouge quasiment pas, ce qui revient à considérer le modèle à 1 ddl de la figure b).
On suppose la tour d'une masse uniformément répartie sur la hauteur. En partant du principe d'équivalence de l'énergie cinétique entre la tour réelle (poutre continue homogène encastrée libre de la figure a) et le modèle simplifié (figure b), montrer que la masse équivalente
("modale") du système discret est
.
Rappel : le premier mode de vibration d'une poutre encastrée libre est, sous forme normalisée : où
est la hauteur de la poutre.
Dans mon cours, j'ai que le raideur d'une poutre en flexion s'écrit .
Par ailleurs, j'ai calculé les raideurs et amortissments équivalents de la figure b) : et
(je ne sais pas si ce sera utile).
Selon moi, l'énergie cinétique de la figure b) s'écrit et celle de a) :
je ne vois pas quoi mettre à la place des petits points et, dans mon cours, je n'ai pas de relation entre l'énergie et les modes de vibrations.
En regardant la figure a), j'ai l'impression que le déplacement latéral de la tour, s'identifie à
Et donc ;
Sinon, le DL en 0 de donne
ce qui fait apparaitre un 8 comme dans la relation demandée mais je ne vois pas vraiment de raison de faire ce DL en 0
Je suis donc un peu bloqué et je ne vois pas comment aboutir à la relation entre les masses...
Merci à vous !
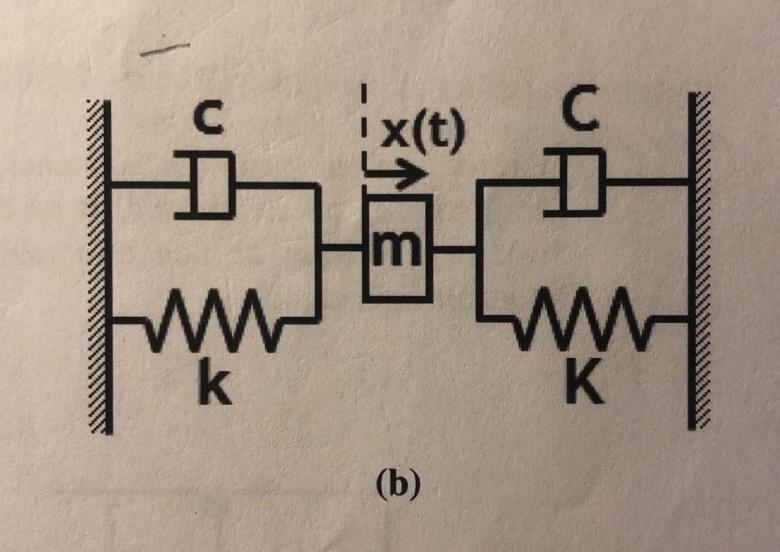
Bonjour,
Vous vous éloignez de la question : la recherche de la masse équivalente revient simplement à dire que les deux énergies cinétiques sont égales. Vous avez donc juste à calculer l'énergie cinétique de la poutre donc on vous donne la vitesse en une point (seul formule utile pour cette partie).
La poutre est un système continu, il faut donc la découper en tronçon dz, calculer l'énergie cinétique de ce tronçon et intégrer.
Bonjour,
merci pour votre réponse.
En suivant vos conseils, j'ai écrit :
donc en intégrant sur la longueur
donc en posant
la masse de la poutre on aboutit bien au résultat donné.
Seul problème, je n'ai pas trop compris ce que j'ai écrit :
- pourquoi est-ce qu'on assimile un mode de vibration à une vitesse ?
- pourquoi est-ce qu'il n'y a pas de terme en ?
Merci pour vos retours,
Bonne soirée
Bonjour,
On n'assimile pas un mode vibration à une vitesse, on cherche la masse équivalente qui ayant la vitesse v0 a la même énergie cinétique qu'une barre vibrant selon le premier mode avec la vitesse maximale v0. La donnée est la vitesse en chaque point de la barre.
Un mode est un terme assez générique qui représente la manière dont le système vibre de manière sinusoïdale, la fréquence correspondante ... Ici on caractérise le mode par sa vitesse.
Il y a un terme en : c'est v(z)2.
Il ne faut pas oublier que la vitesse donnée est normalisée, c'est une vitesse sans dimension : en notant V(z) la vitesse et la vitesse maximale, le v(z) du texte vaut
. Il manque un 1/2 dans votre énergie cinétique mais sans conséquence, et votre Ec est aussi une énergie cinétique adimensionnée.


