Niveau licence

Vibration d'une barre

Posté par
lebihaan2 31-01-21 à 22:27

Bonsoir,
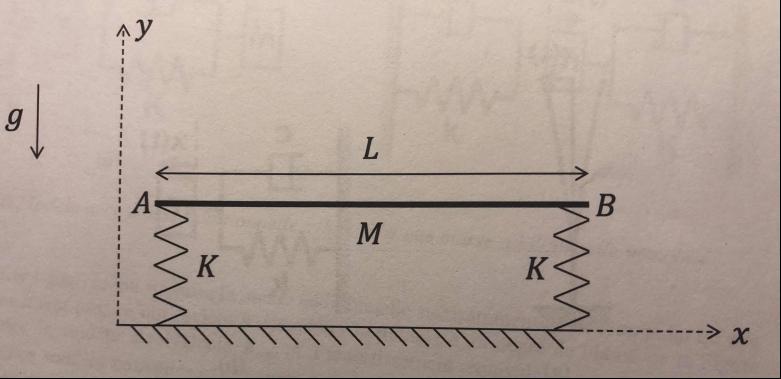
je suis bloqué face à l'exercice suivant : soit une barre AB rigide reposant sur 2 ressorts verticaux (dont la masse est négligée) de raideur K et de longueur au repos $\ell_0$ . (voir la figure)
1) On choisit comme degrés de liberté (ddl) $y_A$ et $y_B$ . A partir des équations de Lagrange, écrire les équations du mouvement. Se placer dans le cadre des petites transformations pour linéariser les expressions obtenues et négliger les déplacements horizontaux. Rappel : pour la barre rigide de masse M et de longueur L, $E_c=\frac{1}{2}Mv^2(G)+\frac{1}{2}\frac{ML^2}{12}\dot{\theta}^2$ où v(G) est la vitesse du centre de gravité et $\theta$ l'angle de rotation de la barre.

2) Définir 2 nouveaux ddl de sorte de s'affranchir de la contribution statique de la gravité dans l'analyse dynamique du système. Ils décriront le mvt de la barre par rapport à la position d'équilibre précédente. Réécrire le nouveau système sous la forme $[M]\{\ddot{X}\}+[K]\{X\}={0}$ avec M et K deux matrices 2x2

3) Calculer les fréquences et modes propres du système

Pour la première question, voilà ce que j'ai réalisé :
Les équations de Lagrange s'écrivent ici : $\frac{d}{dt}\left ( \frac{\partial E_c}{\partial \dot{y}} \right)-\frac{\partial E_c}{\partial y}+\frac{\partial E_p}{\partial \dot{y}}=0$
Avec la formule de Varignon $\vec{v}(G)=\vec{v}_A+\vec{GA}\wedge \dot{\theta}\vec{z}=\left ( \dot{y}_A+\frac{L}{2}\dot{\theta}\right ) \vec{y}=\left ( \dot{y}_B-\frac{L}{2}\dot{\theta}\right ) \vec{y}$ .

Donc $E_c=\frac{1}{2}M( \dot{y}_A+\frac{L}{2}\dot{\theta})^2+\frac{1}{2}\frac{ML^2}{12}\dot{\theta}^2$ et $E_p=\frac{1}{2}K(y_A-l_0)^2+\frac{1}{2}K(y_B-l_0)^2+Mg\frac{y_A+y_B}{2}$

En ce qui concerne l'énergie potentielle de pesanteur, le résultat est intuitif, je ne sais pas le démontrer, mais selon moi, cela correspondant à l'énergie potentielle de pesanteur du centre de gravité.

En appliquant les formules de Lagrange, je trouve pour $y_A$ : $M\left ( \ddot{y_A}(\dot{y_A}-\frac{L}{2}\dot{\theta})+\dot{y_A}(\ddot{y_A}-\frac{L}{2}\ddot{\theta}) \right ) +Ky_A(y_A-l_0)+\frac{Mg}{2}=0$
Mon problème pour la suite est que je ne vois pas du tout comment linéariser mes équations....

Merci d'avance !

$Vibration d\'une barre$

Posté par re : Vibration d'une barre 31-01-21 à 22:36

Bonjour,

Le problème de départ est que vous ne suivez pas le texte qui demande d'exprimer vos équations avec comme variables yA et yB.
Il faut donc se débarrasser de (ne pas oublier "se placer dans le cadre des petites transformations").

Posté par re : Vibration d'une barre 02-02-21 à 00:55

Merci beaucoup ! Après de lourds calculs, j'aboutis à $E_c=\dfrac{M}{6}(\dot{y_A}^2+\dot{y_A}\dot{y_B}+\dot{y_B}^2)$ (peut-être y avait-il un moyen plus simple d'y arriver?) et j'aboutis bien à un système matriciel en définissant 2 nouveaux ddl (j'ai retranché la position d'équilibre aux anciens!)

Ensuite je trouve 2 fréquences propres $\sqrt{\dfrac{6k}{M}}$ et $\sqrt{\dfrac{2k}{M}}$ associées à 2 vecteurs propres orthogonaux !

Encore merci !

Posté par re : Vibration d'une barre 02-02-21 à 09:04

Bonjour,

C'est simplement qqch du genre a(x+y)²+b(x-y)² (après linéarisation), c'est cela que vous appelez lourd ?
La partie non linéaire, il faut juste la poser sans aller plus loin.

Posté par re : Vibration d'une barre 07-02-21 à 22:07

Oui c'est ça que j'appelle lourd, ça faisait une dizaine de ligne de calcul pour arriver aux équations du mouvement !

Merci

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Vibration d'une barre

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique