Inscription / Connexion Nouveau Sujet
via ferrata tension
Bonjour
J'ai un petit sujet a effectuer sur la via ferreta en mecanique/physique
But :
Faire un fichier excel qui permet de tracer des abaques nécessaire au dimensionnemeent des point d'ancrage des filin d'acier utilisés pour securiser les via ferrata.
Je doit determiner la Tension T
f1 : la fleche initiale varie entre 0.2m et 0.6m
p: poids lineique du filin 4N/M
T: Tension dans le filin inconnue en N
F : Charge en cas d'urgence : fixe 7000N
E module de young 6.5E10 Pa
A aire de section du filin 6.5E-5m²
L portée du filin : variable de 2 à 20 m
Formule :
f1 = (p*L²)/(8T1) ou T1 tension initiale du filin
Sa = (L/2) + (p² * L^3)/(48T1²)
cos(a) = (L)/(2Sa*(1+(T/EA)))
cos(a) = (L)/(2Sa*(1+(T/EA)))
T² - (F²)/(4*(1-(cos²(a)))=0
Avec les deux formule ci dessus, normalement en remplacant cos (a) et apres simplification on obtient une equation de degres 4
J'aimerais déterminer T pour :
f1 = 0.2m
L = 2.5m
Donc T1 = (p*L²)/(8*f1)
P = 4N/m (cste)
F=7000N (cste)
A= 6.5E-5m²(cste)
E=6.5E10 Pa (cste)
determiner T avec l'equation ci dessus.
Si vous pouvez m'aider
Merci
G P
***Edit gbm : niveau mis en accord avec ton profil***
Bonsoir,
Je ne sais pas de quelle version d'Excel tu disposes. Si ta version est la version 2003 ou une version postérieure, vérifie par le menu : /outils/macro complémentaires que le complément solveur est bien installé.
Si oui, la résolution d'une équation de degré 4 ne devrait pas te poser de problème
Bonjour
Ok, pour ca il n'y a pas de probleme, le seul hic, c'est que je n'arrive pas a trouver l'equation de degres 4.
et si il serait possible de faire le calcul pour voir si on obtient le meme T. J'obtient T =environ 4000N. A verifier
Merci
Cordialement
G PERRET
Bonsoir,
en éliminant le cosinus entre les deux dernières équations, on obtient l'équation ci-dessous qui peut encore se développer et s'ordonner pour faire apparaître un polynôme de degré 4 en T.
Bonjour,
Petite erreur de retranscription sous TEX ; voici la formule corrigiée :
Les valeurs numériques que tu as fournies conduisent à :
T1=15,625N ; Sa=1,2713m
Les coefficients du polynome de degré 4 sont :
A = 5.602044746332411e-14
B = 4.733727810650888e-07
C = 0.033278302180902
D = -5.798816568047338
E = -12250000
(A : coefficient de T4, B : coefficient de T3 etc...)
La seule solution positive fournie par Matlab est :
T = 17258,231233802N
A toi d'arrondir correctement en fonction de la précision des données...
Merci,
Bon je comprend pas, j'ai du me tromper dans mon calcul.
Merci, je vais refaire mon calcul.
Sinon il y a t'il une solution pour calculer une equation de degres 4. Methode de ferrari...?
Comme ca pour créer ma macro excel qui va permettre de faire la résolution de l'equation se sera plus simple.
Cdt
A bientot
G P
Je n'utilise plus Excel depuis longtemps mais il me semble que certaines versions récentes contiennent une macro utilisant la méthode de Newton, bien suffisante dans ce cas, je pense.
En école d'ingénieur, l'usage de Matlab (ou de sa version gratuite "SCILAB") n'est pas au programme ?
Ok,
merci, pour votre aide.
Etant donner que je suis en première années a l'insa, pouvez vous m'expliquer rapidement la méthode de newton.
Merci
Bonsoir,
Lorsqu'on résous une equation de degres 4, n'y a t-il pas quatre solution avec i (complexe)?
Tout dépend des valeurs respectives des coefficients. Tu as 4 solutions ; certaines peuvent être complexes ; c'est un peu comme les solutions d'une équation de degré deux : l'existence ou non de racines complexes dépend du signe du discriminant...
Pour la méthode de résolution : les deux plus simples sont la méthode de dichotomie et la méthode de Newton ; tu trouveras des explications et des exemples à l'adresse suivante :
Bonjour
Pouvez vous me dire si on obtient l'equation suivante:
(1/(A²+E²))T^4+(2/A*E)T^3+(1-(F²/(4*A²*E²))-(L²/4S²))T²-(F²/2A*E)T-(F²/4)
donc a = (1/(A²+E²))
b= (2/A*E)
c= (1-(F²/(4*A²*E²))-(L²/4S²))
d = (F²/2A*E)
et e = (F²/4)
Merci
Bonjour,
Voici ce que j'obtiens :
Tu as commis une erreur sur a : E2 et A2 doivent être multipliés et non additionnés, sinon le résultat n'est pas homogène.
***Message supprimé***
***Edit gbm : message supprimé pour que vous puissiez poursuivre votre échange, maintenant que l'aide a été apportée pour l'autre sujet***
Bonsoir,
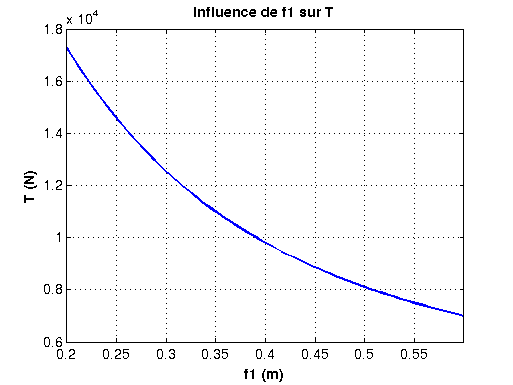
Cela pourra peut-être t'aider : voici la courbe obtenue avec Matlab représentant les variations de T en fonction de f1
(0,2m  f1
f1  0,6m).
0,6m).