Niveau maths spé

Vérification QCM -mécaflu

Posté par
iSirrol 10-10-16 à 14:09

Bonjour

j'ai fait un questionnaire de mécanique des fluides et j'aimerai savoir si mes réponses sont justes :

Question 1 : Quels sont les éléments dans la liste ci-dessous qui se réfèrent à la définition d'une trajectoire ?

Une particuleV
Un ensemble de particulesX
$\dfrac{dx}{u}=\dfrac{dy}{v}=\dfrac{dz}{w}=dt$ V
$\dfrac{dx}{u}=\dfrac{dy}{v}=\dfrac{dz}{w}$ X
Vision lagrangienne du mouvementV
Vision eulérienne du mouvementX

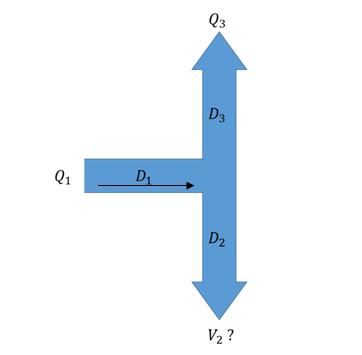
Question 2 : Calculer la vitesse V2 en m/s avec Q1=10l/s, Q3=Q1/4, D1=20mm, D3=D2=15mm (arrondir à l'entier inférieur)
Vérification QCM -mécaflu

$42 m.s^{-1}$

Question 3 : Soit un champ de vitesse V, Quelle est l'équation des lignes de courant associées : v=(u=ωx,v=ωy)

y=C_x
y= $\frac{c}{x}$
y=C_x²
Aucune de ces réponses n'est valable

Cette question est très peu claire et m'est donnée sans plus de précision

Question 4 : Le vecteur vitesse peut se décomposer en termes de :

Translation V
Rotation V
Déformation X
Convolution X
Dissolution X
Transformation X

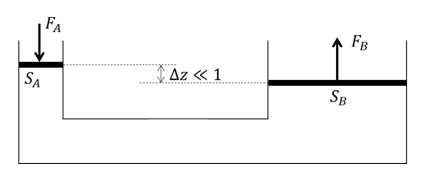
Question 5 : Une presse hydraulique comporte généralement deux pistons de surface différente. En négligeant l'action de la pesanteur et en supposant que les forces sont uniformément réparties sur les pistons, donner la force nécessaire d'appliquer sur un piston de 0.01m² pour soulever une masse de 10 kg posée sur un piston de 1m² ? On prendra g=10m.s^-2
Vérification QCM -mécaflu
FA=1 N X
FA=1 kg X
FA=1000 N V
FA=10 N/m2 X

mon application numérique me donne plutôt 10000 N mais cette réponse n'est pas proposée

Question 7 : Dans un écoulement de fluide parfait incompressible soumis à des forces de masse dérivant d'un potentiel, si une particule fluide a un taux de rotation nul à un instant t donné, comment évolue la valeur de ce taux de rotation pour t →∞ ? :

Il reste nul
Il augmente
Il diminue
Le taux de rotation ne peut pas être nul pour ce type d'écoulement.

Question 15 : Un objet cylindrique se meut sous la surface de l'eau (fluide parfait incompressible) à 10 m de profondeur et à la vitesse constante de 10m.s⁻¹(voir figure)
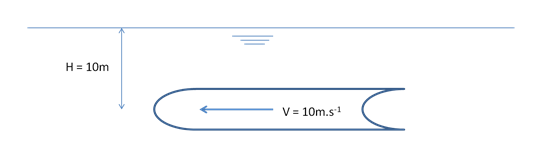
Vérification QCM -mécaflu
En prenant comme référence des hauteurs la surface libre et comme origine des pressions la pression atmosphérique ; la pression qui s'exerce sur le centre du nez de l'objet cylindrique vaut :

0,15 bar X
1,5 bar V
15 bar X
150 bar X
Aucune des réponses proposées n'est correcte X

pour répondre à celle la je n'ai fait aucun calcul mais simplement une détermination par ordre de grandeur usuel, on sait que à 10m de profond la pression est d'un bar de plus qu'à la surface, mais comment trouver les 0.5 restant ?...

Question 16 : On considère le schéma hydraulique ci-dessous où de l'eau (fluide parfait incompressible en écoulement permanent) est pompée dans un lac pour être distribuée dans un réseau d'irrigation en M.

Le pont M est à l'air libre. On considère que la surface du lac est très grande par rapport à la surface du tuyau de distribution. Le débit en volume du fluide en M est Qv=100L.s−1 ; la section du tuyau en M est de 10cm2. En négligeant toutes formes de pertes d'énergie dans le système ; la puissance de la pompe à prévoir pour assurer la circulation du fluide est de :

2,5 W
25 W
250 W
2500 W
Aucune des réponses proposées n'est correcte

Mon application numérique me donne une énergie volumique $2.5\times 10^5J.m^{-3}$ comment passer à une puissance ? j'ai penser le multiplier par le débit (ce qui serait homogène) mais dans ce cas aucune réponse ne convient

Je n'ai pas répondu aux questions 3, 7 et 16 car je ne pense pas que les réponses proposées soient correctes

merci à celui ou celle qui prendra le temps de m'aiguiller

Posté par re : Vérification QCM -mécaflu 10-10-16 à 14:20

oubliez la question 3, c'est une erreur d'affichage

Posté par re : Vérification QCM -mécaflu 10-10-16 à 16:08

Bonjour
Quelques indications :
OK jusqu'à 4 (sauf 3 ???)
Pour 5 : l'influence de la pesanteur étant négligée, la pression du fluide est à même au niveau de chaque piston en régime permanent ou quasi permanent : $\frac{F_A}{S_A}=\frac{F_B}{S_B}$ . Cela conduit à F_A de l'ordre de 1N. Cet exercice illustre le principe des presses hydrauliques.
Pour 15 : il faut appliquer la relation de Bernouilli : les 0,5 bar qui te manque correspondent au terme en $\frac{1}{2}\rho V^{2}$ .
Pour 16 : la puissance est le produit de l'énergie massique par le débit massique. Pour un fluide incompressible, c'est aussi le produit du débit volumique par l'énergie volumique.
Pour la 7 : j'avoue ne pas très bien comprendre. Peut-être faut-il écrire l'accélération particulaire sous la forme : $\frac{\partial\overrightarrow{V}}{\partial t}+\frac{1}{2}\overrightarrow{grad}\left(V^{2}\right)+\overrightarrow{rot}\left(\overrightarrow{V}\right)\wedge\overrightarrow{V}$ puis la force massique sous la forme d'un gradient d'un champ scalaire... ?

Posté par re : Vérification QCM -mécaflu 10-10-16 à 16:12

super !

merci pour les précisions je comprend mieux mes erreurs

Posté par re : Vérification QCM -mécaflu 10-10-16 à 22:53

Quelques précisions sur la 7 : on part de :
$\frac{\partial\overrightarrow{V}}{\partial t}+\frac{1}{2}\overrightarrow{grad}\left(V^{2}\right)+\overrightarrow{rot}\left(\overrightarrow{V}\right)\wedge\overrightarrow{V}=-\overrightarrow{grad}\left(ep\right)$
Il s'agit d'étudier l'évolution au cours du temps de $\overrightarrow{\Omega}=\overrightarrow{rot}\left(\overrightarrow{V}\right)$ .
On prend le rotationnel de chaque terme de l'égalité. Sachant quele rotationnel d'un gradient est le vecteur nul et que le rotationnel d'une dérivée par rapport au temps est égal à la dérivée par rapport au temps du rotationnel, cela donne :
$\frac{d\overrightarrow{\Omega}}{dt}+\overrightarrow{rot}\left(\overrightarrow{\Omega}\wedge\overrightarrow{V}\right)=\overrightarrow{0}$
Si le vecteur $\overrightarrow{\Omega}$ est susceptible de dépendre du temps mais pas des coordonnées d'espace, la formule précédente conduit à un vecteur $\overrightarrow{\Omega}$ fixe au cours du temps.

Posté par re : Vérification QCM -mécaflu 12-10-16 à 14:26

Question 3 : Soit un champ de vitesse V, Quelle est l'équation des lignes de courant associées : v=(u=ωx,v=ωy)

$y=C\times x$
$y=\dfrac{C}{x}$
$y=C\times x^2$
Aucune de ces réponses n'est valable

voilà comment il faut lire la question

Posté par re : Vérification QCM -mécaflu 12-10-16 à 14:51

La réponse à la 3 est donc:

réponse A : $y=C\times x$ V en intégrant en $\ln$

Question 7 : Dans un écoulement de fluide parfait incompressible soumis à des forces de masse dérivant d'un potentiel, si une particule fluide a un taux de rotation nul à un instant t donné, comment évolue la valeur de ce taux de rotation pour t →∞ ? :

Il reste nul V
Il augmente X
Il diminue X
Le taux de rotation ne peut pas être nul pour ce type d'écoulement. X

d'après les précisions que tu donnes vanoise

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Vérification QCM -mécaflu

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique