Bonjour,

Tu trouveras tout ce qu'il te faut ici --> Mouvement d'un projectile dans le champ de pesanteur

Et tu pourras alors si tu le juges utile revenir proposer tes solutions ou bien poser des questions précises sur ce qui te pose problème.

Merci d'avoir m'aider. J'ai trouvé le sommet de coordonnées (0;0) en ce point le vecteur vitesse est nul.

Pour pouvoir t'aider j'ai besoin de savoir comment tu as obtenu les coordonnées du sommet et la valeur du vecteur vitesse en ce point.

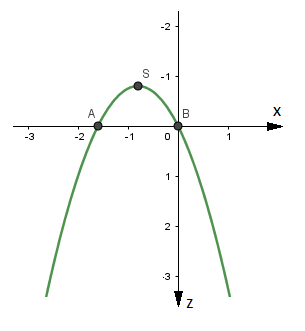
J'ai représenté l'équation de la trajectoire qui est Z=(5/4)x^2+2x dans le repère (o, i, j, k).
En posant que z=0 reviens à dire que (5/4)x^2+2x=0 et j'ai trouvé (0;0) et (0; -1,6) donc le point de coordonnées (0;0) correspond le sommet de la trajectoire.

L'expression du vecteur vitesse est √[(Vi)^2+(Vj)^2] or temps est égal à zéro en ce même point de coordonnées (0;0).

D'accord avec toi en ce qui concerne l'équation de la trajectoire :
z(x) = (5/4)x² + 2x

Mais en écrivant que z(x) = 0 tu trouves les coordonnées des intersections de z(x) avec l'axe des abscisses alors que tu recherches les coordonnées du sommet de la trajectoire.

Oui après avoir résoudre l'équation z(x)=0 puis j'ai donné des valeurs arbitraires à x en tenant compte des conditions de l'exercice c'est-à-dire l'axe (zk)>0

Connaitre les coordonnées du sommet S de la trajectoire n'est pas indispensable pour répondre
à la question 2a)
Toutefois on peut en effet rechercher ces coordonnées et à partir de là trouver ce qui est demandé même si ce n'est pas la méthode la plus simple.

Pour calculer les coordonnée de S :
L'abscisse x_S du sommet S de la trajectoire s'obtient à partir de la valeur de x qui annule la dérivée de l'équation de la trajectoire.
Une fois  x_S connu on en déduit facilement la valeur de y_S