Inscription / Connexion Nouveau Sujet
Utilisation d'un bras de levier
Bonjour,
Voici un petit exercice concernant un chapitre de mécanique autour du théorème du moment cinétique pour un point matériel qui me pose pas mal de soucis :
Tom utilise un bras de levier afin de soulever un rocher de masse M = 200 kg. On donne les valeurs numériques des longueurs d1 = 50 cm , et d2 = 1,5 m ainsi que l'angle  = 60°. On admet que le rocher commence à se soulever lorsque le moment de la force exercée par Tom par rapport à l'axe (O, ux) est supérieur ou égal (en valeur absolue) à celui du poids du rocher.
= 60°. On admet que le rocher commence à se soulever lorsque le moment de la force exercée par Tom par rapport à l'axe (O, ux) est supérieur ou égal (en valeur absolue) à celui du poids du rocher.
1) Tom se suspend au levier. Quelle doit être sa masse minimale pour que le rocher se soulève ?
2) Tom décide d'optimiser son action sur le levier. Dans quelle direction doit-il exercer une force pour être le plus efficace ? Quelle doit être la valeur minimale de cette force ?
Pour visualiser le problème voici un petit schéma :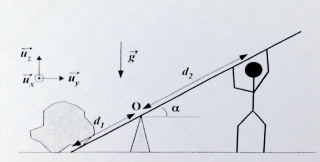
Concernant la première question, j'ai "traduit" la condition pour que le rocher se soulève par le fait que
M (f)
(f)  M
M (P)
(P)
avec f la force exercée par Tom et P le poids du rocher.
Là, premier souci, je ne comprends pas très bien comment exprimer la force exercée par Tom. J'ai supposé qu'elle pouvait être son propre poids pour continuer (ne voyant pas d'autre solution pour avancer).
J'ai donc exprimé les deux moments, en notant R le point relatif au rocher et M le point matériel relatif au point d'appui de Tom :
M (f) = OR
(f) = OR  (-Mg.uz).u
(-Mg.uz).u = d1.Mg.cos(
= d1.Mg.cos( ).u
).u
M (P) = OM
(P) = OM (-mg.uz).u
(-mg.uz).u = -d2.mg.cos(
= -d2.mg.cos( .u
.u
A partir de là, j'ai repris mon inégalité, et en remplaçant par les expressions j'ai trouvé m  M.d1/d2
M.d1/d2
Avec l'application numérique, je trouve m = 66kg, ce qui ne parait pas abérrant, mais je pense avoir fait une erreur du fait que l'angle  n'intervienne plus à la fin.
n'intervienne plus à la fin.
Pour la seconde question, je pense que la force devrait être exercée le plus "loin" possible de O, mais je ne vois pas du tout comment m'y prendre pour trouver la force minimale.
Si une âme charitable avait une petite idée pour débroussailler tout cela, je lui en serais très reconnaissante 
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
bonjour,
J'ai supposé qu'elle pouvait être son propre poids pour continuer (ne voyant pas d'autre solution pour avancer).
bien supposé

effectivement quand tu te pends à un levier, le levier est soumis à ton poids (what else?)
pour la seconde question, attention, on suppose que OM ne varie pas (OM=d2) et on cherche à optimiser l'effet de levier en M
Bonjour,
tu as répondu correctement à la première question. Les forces exercées par le rocher et Tom sont toutes les deux verticales et forment donc un même angle avec la barre, c'est pour ça qu'il n'intervient pas ici.
Pour la seconde question, tu vois bien que si Tom applique une force verticale, qu'on peut écrire sous la forme :
( et
sont définis comme dans le schémas ci-dessous)
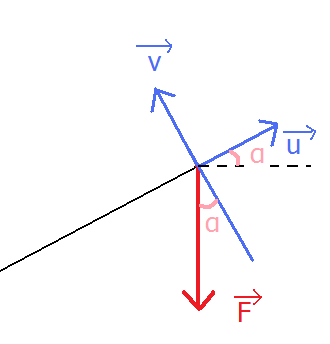
la partie de la force qui est colinéaire au bras de levier est "perdue", elle ne contribue pas au moment :
.
Comment diriger la force appliquée par Tom sur le levier pour qu'elle soit entièrement mise à contribution pour le moment en O ?
Merci beaucoup à vous deux pour vos réponses super rapides et claires 
@ krinn
D'accord, je n'avais pas bien saisi que la distance d2 devait être fixe, ça éclaire un peu mieux la question comme ça, merci !
@ athrun
Ah oui je comprends mieux pourquoi l'angle d'intervient plus alors, je n'avais pas saisi cela, merci !
Pour la seconde question, je pense avoir compris. Il faudrait que la force exercée par Tom soit uniquement dirigée perpendiculairement au bras de levier donc ?
Une idée pour la fin de la réponse de la question 2 : en supposant que la force exercée par Tom est optimisée pour que son action sur le levier soit "utile", on peut peut être écrire que
M (f) = M
(f) = M (f
(f
 ) = -d2.IIf
) = -d2.IIf
 II = -d2.IIfII
II = -d2.IIfII
En re-injectant dans l'inégalité de la condition de soulèvement du rocher, on obtient :
d2.IIfII  d1.Mg.cos(
d1.Mg.cos( )
)
d'où IIfII  d1Mgcos(
d1Mgcos( )/d2
)/d2
Je m'excuse pour les symboles des normes qui font assez mal aux yeux, je ne maîtrise pas du tout l'outil très élégant qui est proposé en module 


