Inscription / Connexion Nouveau Sujet
Une question transfert thermique
Bonsoir, j'ai besoin d'aide avec une question sur le transfert thermique :
La température d'extraction pour un expresso est de 85°C. Il faut une dégustation du café à 65 °C. (il y a d'autres informations mais qui ne servent pas je pense...
1) Utiliser les outils du logiciel tableur grapheur pour vérifier que l'équation de la courbe tracée peut être modélisée par une fonction de la forme :
teta(t) = (tetai - tetaf ) . e^(-t/to) + tetaf avec tetaf = tetaTh température de l'air ambiant (le thermostat).
Déterminer les valeurs de tetai , tetaf et to. Vérifier la valeur de to en utilisant une autre méthode.
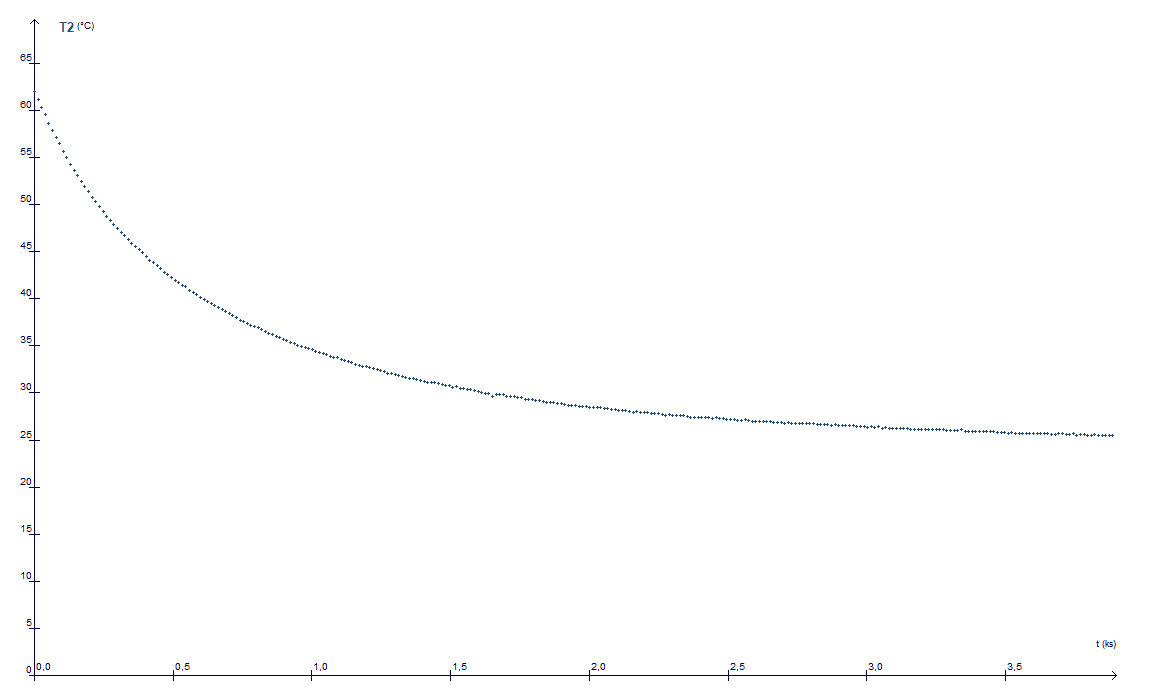
Voici le graphique (je n'ai pas mis le tableur car trop long). La température la plus haute est 62 C et la plus basse 24,43. Donc tetai= 62 et tetaf=24,43 ? Ou 62-24.34 ? Pour déterminer to, je connais la méthode de l'asymptote mais quelle est l'autre méthode ? Je ne comprend pas ce qu'il faut faire pour le début de la question concernant la vérification...
Merci d'avance
Bonsoir
Isole l'exponentielle d'un côté du signe "=" puis écrit l'égalité des logarithmes neperiens des deux termes. Representer les variations en fonction du temps d'un logarithme doit donner une droite dont le coefficient directeur dépend de la constante de temps.
ln(e^(-t/to))=ln((teta(t)-tetra)/(terai-tetaf))
-t/to= ln((teta(t)-tetra)/(terai-tetaf)) ?
Mais je dois utiliser les outils du logiciel non ?
Bien vu ! Ajoute une nouvelle colonne à la feuille de calcul de ton tableur pour y calculer pour les différentes valeurs de t, le logarithme. Ensuite crée un nouveau graphique avec t en abscisse et le log en ordonnée. Ensuite : utilise le programme de régression linéaire du tableur pour obtenir l'équation de la droite moyenne qui te fournira la constante de temps.
Si tu n'y arrives pas, scanne et poste ici le tableau de valeurs. Je t'aiderai.
Je viens juste de lire ceci écrit : « Remettre l?exploitation sur une feuille manuscrite. », je dois donc faire aussi sur feuille ou imprimer les courbes?
Je n?ai pas bien compris le but de refaire une autre courbe.
Voici le lien du fichier permettant d?afficher la courbe (sur atelier scientifique) : https:/******Je ne sais pas ce que vous entendez par scanner, c?est une acquisition d?une heure je crois avec 1 point tout les 20secondes donc c?est assez mon?
***lien supprimé***merci de mettre l'image directement dans ton message****
Il s'agit bien d'utiliser une autre méthode pour obtenir la constante de temps ?
Je t'en ai fournie une, assez rapide grâce au tableur...
Ah d'accord, je pensais que ça allait être une méthode que je connaissais, je n'ai jamais utilisé la « régression linéaire »
Et ne sais pas quoi mettre dans la nouvelle colonne, tout le ln((teta(t)-tetra)/(terai-tetaf)) ?
D'accord merci mais donc qui est t'étage et tetai, est-ce que j'ai eu bon dans ce que j'ai dit ? Pour t=0, on a 62 degrés et pour t=3900s (donc la fin), on a 24,43 degrés donc tetai=62 et tetaf=24,43 ? Ou tetai-tetaf=24,43 ?
 i est la température à la date t=0, c'est à dire la température de la première mesure effectuée : 62°C apparemment.
i est la température à la date t=0, c'est à dire la température de la première mesure effectuée : 62°C apparemment.
 f n'est pas la température de la dernière mesure effectuée mais la température que l'on atteint au bout d'un temps très long, lorsque l'équilibre entre le liquide et l'air ambiant est réalisée. C'est l'ordonnée de l'asymptote à l'exponentielle, c'est aussi la température ambiante qui a j'espère été mesurée.
f n'est pas la température de la dernière mesure effectuée mais la température que l'on atteint au bout d'un temps très long, lorsque l'équilibre entre le liquide et l'air ambiant est réalisée. C'est l'ordonnée de l'asymptote à l'exponentielle, c'est aussi la température ambiante qui a j'espère été mesurée.
Quel logiciel utilises-tu ?
Atelier scientifique. Vers la fin, les valeurs de teta semblent être constantes, pour une valeur d'environ 24,43 donc c'est ça non ? L'air ambiant n'est pas donné (on donne un air ambiant à une question suivante mais avec laquelle je n'ai pas besoin d'aide)
Vers la fin, les valeurs de teta semblent être constantes, pour une valeur d'environ 24,43 donc c'est ça non ?
Approximativement : oui. Pour une meilleure précision : il faudrait modéliser la courbe par une exponentielle : cela semble correspondre à ta première méthode.
Je ne peux pas vérifier tes résultats car le fichier .lab de Jeulin que tu as posté n'est pas exportable sans le mot de passe Jeulin ...
Mais 24,43 ne serait pas plutôt tetai-tetaf au lieu de tetaf ? Puisque la valeur de la fin est celle initial - celle final non ?
Ah bon, j'ai téléchargé le fichier depuis le lien que j'ai envoyé et je l'ouvre sans problème, j'ai téléchargé le « logiciel Atelier scientifique élevé physique-chimie » soit le premier lien Google… Le lien a été supprimé car on me demande une photo mais il en faudrait sans doute une dizaine voir trentaine pour envoyer toute les valeurs du tableur… En tout cas, comment faut-il répondre à cette question : vérifier que l'équation de la courbe tracée peut être modélisée par une fonction de la forme ?
Bonjour à vous deux,
Lilooo, moi aussi j'ai essayé de télécharger...impossible...je ne connais pas ce type de fichier ? peux-tu l'exporter en pdf ? là en mettant un lien, je pourrais le récupérer ...
Bonjour, .lab c'est pourtant le format utilisé par le logiciel atelier scientifique élève, si vous enregistrez un fichier avec atelier scientifique élève, vous verrez qu'il sera sous ce format là, je ne pense pas qu'on puisse le convertir en pdf, j'ai essayé mais le pdf devient inutilisable...
Je ne peux pas vérifier tes résultats car le fichier .lab de Jeulin que tu as posté n'est pas exportable sans le mot de passe Jeulin ...
Lilooo, tu as ce mot de passe ?
Non, j'ai téléchargé le fichier depuis le lien envoyé puis je le lance dans le logiciel sans que l'on le demande de mot de passe. C'est le logiciel atelier scientifique ou le site qui héberge le fichier qui demande un mot de passe ?
Bonjour mmalou, Bonjour Lilooo,
Jeulin est à l'expérimentation assisté par ordinateur, ce que Microsoft est à l'informatique en général...
L'idéal ici, serait d'exporter le fichier de donnée dans un format lisible par un tableur classique, type Excel... Cela est possible apparemment avec le mot de passe...
Je vais essayer ce soir de mettre les valeurs du tableur dans un fichier Excel… Pour l'instant, est-ce que vous pouvez répondre à mes questions (sur tetaf et la vérification)
Pour  f : j'ai répondu dans mon message du 20-05-21 à 11:17.
f : j'ai répondu dans mon message du 20-05-21 à 11:17.
Pour la vérification par une autre méthode, je t'ai aussi proposé une autre méthode. Tu calcules pour chaque valeur de t la grandeur :
Dans un nouveau graphique, tu portes en abscisse t, en ordonnée Y. Si la loi exponentielle est bien vérifiée, tu vas obtenir des points alignés avec l'origine du repère. Le coefficient directeur de la droite moyenne vaut (1/to).
Tout cela est très rapide avec le logiciel.
Non ce n'est pas la vérification de to par une autre méthode que je parle, mais de ça : « Utiliser les outils du logiciel tableur grapheur pour vérifier que l'équation de la courbe tracée peut être modélisée par une fonction de la forme » donc ça n'a pas de rapport avec To.
Voici le lien du fichier Excel où j'ai mis toute les valeurs du tableur, vous devriez pouvoir copier toute ces valeurs et les coller dans le tableur de l'atelier.
https://we.tl/t-SrG1aKBK2H
J'ai bien réussi à ouvrir le fichier et à l'importer. Merci ! Les mesures ne sont pas excellentes... La courbe a bien l'allure d'une exponentielle mais en pratique, quand on cherche l'équation d'une exponentielle passant aux plus près des points expérimentaux, les résultats sont assez moyens...
Pour la première question : as-tu appris à modéliser une courbe avec ton logiciel ?
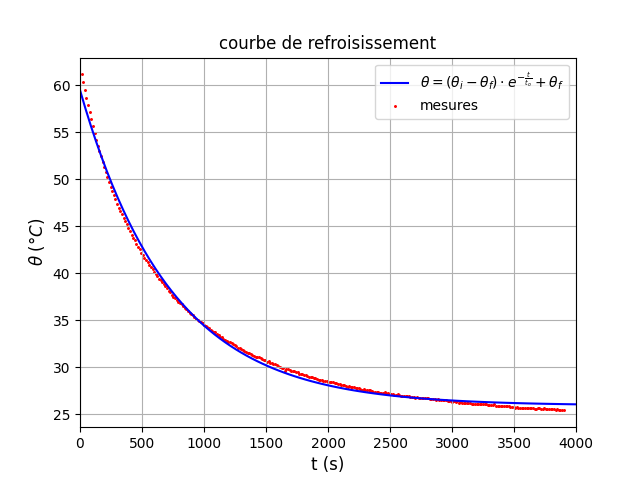
Le menu "modélisation" de ton logiciel doit permettre de tracer l'exponentielle passant au plus près des points expérimentaux. Voici ce que j'obtiens : les points rouges sont les points expérimentaux, la courbe bleue est l'exponentielle. Mon logiciel fournit :
to= 729s (valeur assez proche de celle obtenue par la méthode des tangentes)
 i=59,6°C
i=59,6°C
 f=25,9°C
f=25,9°C
Les résultats sont de qualité correcte mais pas hyper précis. L'exponentielle ne passe pas exactement par le point correspondant à la température initiale (61°) et l'asymptote à l'exponentielle est un peu au dessus de l'asymptote réelle. Mais bon : ce n'est pas si mal vue la qualité du matériel Jeulin ! 
Ah donc quand on demande to, il suffit de lire la valeur donné par le logiciel et la seconde méthode c'est avec la méthode des tangente et asymptote ?
Pour modéliser une courbe, je ne m'en souviens plus mais je crois l'avoir fait…
J'ai fait une modélisation exponentielle décroissante mais ça ne fonctionne pas, (j'ai juste ouvert le fichier de la courbe puis j'ai été dans modélisation puis équation différentielle premier ordre puis j'ai sélectionné exponentielle décroissante puis le bouton modéliser)
mais ça ne fonctionne pas,
Normal : le simple modèle "exponentielle" correspond aux exponentielles d'équations :
où A et b sont deux constantes positives ou négatives.
Je ne connais pas ton logiciel mais de nombreux logiciels de ce genre possède le modèle "charge ou décharge d'un condensateur" qui s'adapte facilement à la situation . Sinon, tu dois sans doute avoir le modèle "autre fonction" qui te permet d'entrer n'importe quelle fonction.
Ah c'est bon j'ai réussi… Cela affiche quelque chose de la forme a+b*e^(-t/to) et a=25,43 b=36,57 et to=719s
Cependant, à quoi correspondent a et b ici ? Ce n'est pas de la forme (tetai-tetaf)*e^(-t/to)+tetaf ?
Donc tetai=60 ?
Et donc dire qu'on a une courbe de la forme a+b*e^(-t/to) et en donnant les valeurs de a et b et en les identifiants ça répond à la question ?
Selon ton logiciel :
 f=a=25,4°C
f=a=25,4°C
 i=a+b=62,0°C
i=a+b=62,0°C
to=719s
Tout cela me parait assez cohérent. Reste à superposer les courbes.
Ah bon, je vais regarder ça, et donc à quoi sert de les superposer, dire que la courbe expérimentale est très proche de son modèle donc il s'agit bien d'une courbe de la forme (tetai-tetaf)*e^(-t/to)+tetaf ?
Oui !
Réflexion faite à propos de la suite sur la deuxième méthode de détermination de to. Celle que je t'ai proposée est peut-être un peu compliquée. Tu peux sans doute te contenter de vérifier que la tangente à la courbe en t=0 rencontre l'asymptote horizontale à la date to ; c'est la méthode que tu as proposée dès le début il me semble.


