Inscription / Connexion Nouveau Sujet
une bille qui "bouche" un bassin - thermo.
Bonjour,
Une sphère de bois de masse volumique  et de rayon R est complètement immergée dans un bassin d'eau, de masse volumique
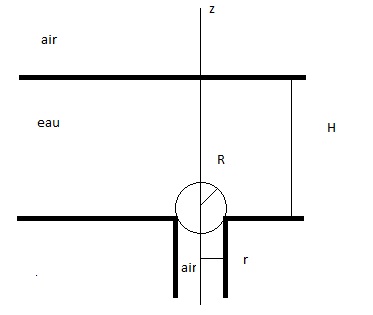
et de rayon R est complètement immergée dans un bassin d'eau, de masse volumique  e de profondeur H de telle manière qu'elle bouche un trou circulaire de rayon r. J'ai essayé de représenter le plus fidèlement le schéma. On me demande de calculer la force que la sphère exerce sur le fond du bassin. Il y a pas mal de trucs que je ne comprends pas dans la correction:
e de profondeur H de telle manière qu'elle bouche un trou circulaire de rayon r. J'ai essayé de représenter le plus fidèlement le schéma. On me demande de calculer la force que la sphère exerce sur le fond du bassin. Il y a pas mal de trucs que je ne comprends pas dans la correction:
La pression en un point de cote z dans l'eau est donnée par P(z) = Pa +  eg(H-z). En fonction de l'angle
eg(H-z). En fonction de l'angle  des coordonnées sphériques, on obtient:
des coordonnées sphériques, on obtient:
P( ) = Pa +
) = Pa +  eg(H+R(cos
eg(H+R(cos 0-cos
0-cos )), où
)), où  0 représente la valeur de
0 représente la valeur de  au niveau de l'ouverture circulaire.
au niveau de l'ouverture circulaire.
OK mais l'angle situé entre n'a-t-on pas aussi le terme en -Rcos ?
?  étant compris entre
étant compris entre  0 et le
0 et le  = pi/2?
= pi/2?
De même, on me dit que dFz= (P( ) - Pa)x(-cos
) - Pa)x(-cos )dS)). Je ne comprends pas le terme en gras.
)dS)). Je ne comprends pas le terme en gras.
Merci.
Bonjour marsmallow,
J'ai un peu la flemme d'expliquer. Donc, je vais le faire. Je te fais la version complète et mathématiques. Suivant ton cours, ça peut être plus simple.
On part d'un élément de surface en coordonnée sphérique, vect(dS) = r²*sin(theta)*dtheta*dphi.vect(Ur).
En remarquant que la pression est invariante suivant vect(Uphi), on peut former un nouvelle élement de surface par intégration de phi.
vect(dS') = 2pi*r²*sin(theta)*dtheta*2*cos(théta)*vect(Uz) = 2*pi*r²*sin(2*theta)*dthéta.
On a un élément de surface d'isopression. Il nous reste à déterminer la pression
P(theta) = Pa + peau*g*(H-sqrt(R²-r²) - R*cos(théta)) si théta app à [0,pi/2+acos(r/R)[
P(théta) = Pa si théta app à [pi/2+acos(r/R),pi]
Avec vect(F) = int(P(théta)*(-dS),théta=0,theta=pi).vect(uz)
Je te laisse faire les calculs. Il se font bien.
Mais si tu bloques dis le nous.