Inscription / Connexion Nouveau Sujet
Un ressort dans un funiculaire
Bonjour
je bloque actuellement sur la première question d'un exercice où l'on s'interesse à un ressort dans un funiculaire. Après avoir fait le pfd sur les deux axes je n'arrive pas à exprimer l'angle 
en fonction du reste. Voici l'énoncé et merci d'avance !
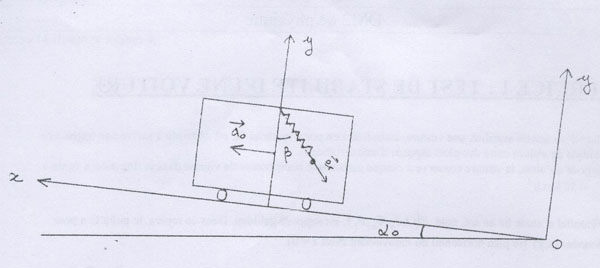
On considère un funiculaire gravissant une pente faisant un angle 0 avec l'horizontale.
Il possède un mouvement de translation rectiligne d'accélération contante a0. On note ex le vecteur unitaire dans le sens de la translation et ey celui perpendiculaire au sol. A l'instant t=0, le funiculaire est en O, origine du repère cartésien.
Un système formé d'un ressort (constante de raideur k, longueur à vide l0) auquel est fixé un objet ponctuel de masse m est suspendu au plafond du funiculaire.
1) Définir le référentiel et le système, puis faire un bilan des forces. Exprimer ces forces dans le repère cartésien (O, ex, ey). On notera l la longueur du ressort.
2) En utilisant la relation fondamentale de la dynamique, déterminer l'angle que fait l'axe du ressort avec la normale au plafond (-ey) en fonction de g,0 et a00.
3) Pour quelle valeur de l'accélération l'angle est-il nul ?
4) Déterminer l'expression de la tension du ressort, puis en déduire celle de la longueur l du ressort.
Pardon j'ai fais une erreur pour la question 2), il faut determiner en fonction de g, 
0 et a ( acceleration )
Bonjour,
Est-ce que tu pourrais nous montrer un schéma ainsi que la projection des forces dans le référentiel que tu as choisi, qu'on sache où tu en es ?
bonjour,
bon commencement, il faudra juste faire un zoom sur le système (ressort + masse), y indiquer les forces et bien reporter les axes et les angles pour ne pas se planter dans les projections
Je n'arrive plus à reposter l'image avec les modifications mais quand j'applique la relation fondamentale de la statique
P+T+m*a(funiculaire/terre)=0
en projetant sur Ox :
-m*g*sin()+k(leq-l0)sin()-m*a(funiculaire/terre)=0
sur Oy :
-m*g*cos()+k(leq-l0)*cos()=0
et après je n'arrive pas trop à voir comment dégager l'angle
et après je n'arrive pas trop à voir comment determiner l'expression de l'angle en fonction des données du problème , à savoir g, 0 et a
tu ne vois rien parce que tu développes trop vite les formules P=mg, F = k
l
et on ne voit plus rien
on a:
-Psin a + F sin b = ao
-Pcos a + F cos b = 0
donc
F sin b = ao + P sin a
F cos b = P cos a
on y voit un peu mieux là, non?
sauf erreur
A mon avis tu y es presque,
Isole sin dans la 1re équation, cos dans la 2e
et le rapport de donnera la tangente de l'angle en fonction des bonnes données.
Annuler
connectez vous