Bonjour à tous,

J'ai un DM de physique portant sur l'optique géométrique, et je bloque sur une question:

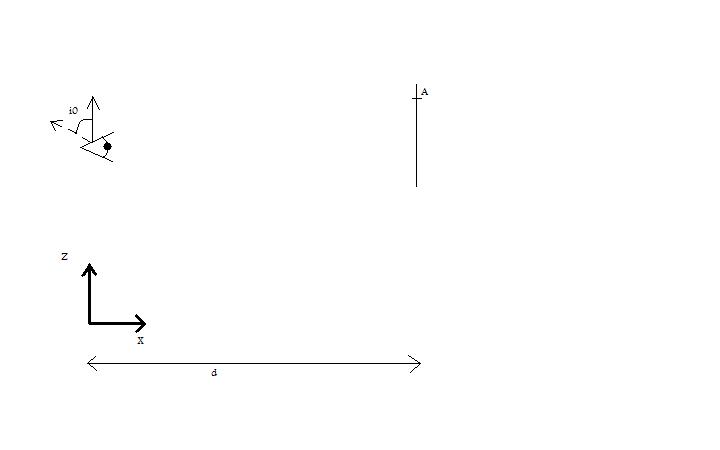
La variable z représente l'altitude, x repère la position horizontale. On considère un objet A, d'altitude zA, et l'oeil d'un observateur situé à la distance d. On admet que les rayons lumineux entre le point de l"objet A et l'oeil de l'observateur suivent une parabole de la forme :
z(x)= x²(k/(4sin²(i0)) - (x/tan(i0)) + z0, k étant une constante positive, i0 la valeur de l'angle entre l'axe vertical et la tangente au rayon au niveau de l'observateur, et z0 l'altitude de l'oeil de l'observateur (de coordonnées (x=0,z=z0)).

On me demande alors de montrer qu'il existe deux valeurs possible de i0, et donc deux paraboles distinctes, si la différence d'altitude z=zA-z0 entre le point A et l'observateur vérifie la condition:
z > (kd²)/4 - 1/k

Dans cette question on peut poser =1/tan(i0)

J'ai exprimé l'équation donnée sous la forme d'un polynôme de second degrés de variable , en considérant l'altitude zA, ce qui me permet de remplacer x par d. Comme 1/sin²(i0) = (1+tan²(i0))/(tan²(i0)) = ²(1+tan²(i0)), on obtient alors:
²[(k(1+tan²(i0))d²)/4] - d - z = 0

Puis pour trouver la condition sur z, je suis parti du principe qu'il existait deux différents et donc deux valeurs de i0 différentes si le discriminant de l'équation était positif. Mais au final je ne m'en sors pas, j'ai cette tangante de i0 qui m'empêche de faire quoi que ce soit...

Bref si vous pouviez me débloquer un peu, trouver ce qui ne va pas dans mon raisonnement, je vous en serais très reconnaissant.

Merci d'avance