Inscription / Connexion Nouveau Sujet
Un peu de filtrage
Bonsoir.
Je bloque en ce moment sur un exercice de filtrage.
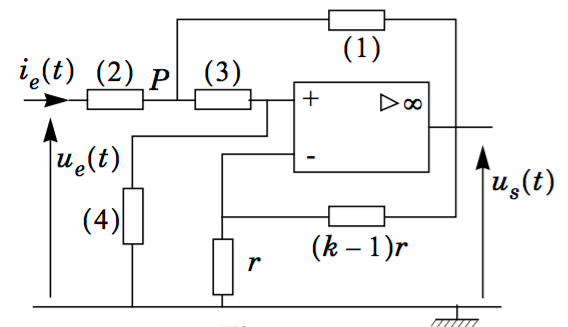
Je joins dans mon message le circuit considéré.
Dans ce filtre, on considère que les dipôles (1) et (2) sont des résistors , (3) un condensateur de capacité C, (4) une association en parallèle d'un condensateur C et d'un résistor R.
On donne la fonction de transfert :
où les Yi sont les admittances complexes des dipôles et k un réel compris strictement entre 1 et 5.
On me demande de mettre la fonction de transfert sous la forme :
et de donner les expressions des différents paramètres.
J'arrive à quelque chose dont je ne suis toutefois pas sûre (en particulier, je crains avoir fait des erreurs de signe, mais j'ai beau vérifier, je ne trouve pas l'erreur) :
Si vous pouviez m'aider à ce sujet...
D'autre part, une petite anecdote dont j'aimerais connaître la réponse : qu'est-ce que la stabilité d'un filtre ?
Un grand merci par avance pour toutes vos réponses à venir, j'espère 
Bonsoir
En posant :
La formule de la fonction de transfert (pas drôle : on ne demande pas de la démontrer !) conduit à :
On divise tous les termes par
pour faire apparaître un 1 au dénominateur en même temps qu'une constante au numérateur :
Je te laisse réfléchir à tout cela et continuer seule. Je pense que le plus dur est fait !
Tu as dû étudier comment obtenir l'équation différentielle vérifiée par la tension de sortie à partir de la fonction de transfert... Si, pour une tension d'entrée constante, la solution de cette équation différentielle tend vers une constante, le filtre est qualifiée de stable. Si la solution de cette équation tend vers 
, le filtre est instable. La tension tend en réalité vers une saturation de l'ampli. OP. De plus, si comme ici, une liaison par résistance existe à la fois entre l'entrée - de l'AO et sa sortie et entre l'entrée + et sa sortie, l'ampli. op. risque de ne pas fonctionner en régime linéaire... Cela est assez compliqué et sans doute pas à ton programme : en général l'énoncé précise si l'ampli op fonctionne ou non en régime linéaire.
Annuler
connectez vous