Inscription / Connexion Nouveau Sujet
Tunnel à travers le globe terrestre
***Bonjour***
La terre est assimilée à une sphère homogène de centre O et de rayon R. Soit g0 la valeur de
l'accélération de la pesanteur à la surface de la terre. On ne tient pas compte de la rotation de la
terre.
On relie deux villes A et B par un tunnel rectiligne de longueur d. Un train assimilable à un point
matériel M se déplace sans frottement dans le tunnel. On note r la distance OM.
Le référentiel terrestre ?0 est considéré comme galiléen ; il est rapporté au repère (I,x0,y0,z0).la force de gravitation éxércé est F=-mg0*r/R
1/ par application de PFD determiner l'équation differentielle du mvmt en x ainsi que la réaction
2/détérminer l'équation horaire x(t)
3/détérminer la vitesse maximale de M en qu'elle point l'est-elle?
4/détérminer l'énérgie potentielle du point M
***Merci d'avance***
***Edit gbm : la politesse n'est pas optionnelle, de même que la recherche d'un exercice***
Coller un énoncé de cette façon est un peu cavalier ... 
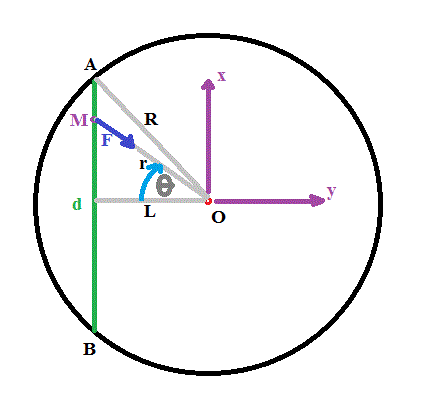
1a)
R² = (d/2)² + L²
L = (V(4R²-d²))/2
Composante de F suivant la direction de Ox : Fx = |F|.sin(theta) = m.go.r/R * sin(theta)
L = r.cos(theta)
r = L/cos(theta) = (V(4R²-d²))/(2.cos(theta)
Fx = m.go.L/R * sin(theta)/cos(theta)
Fx = m.go.L/R * tg(theta)
Or x = - L.tg(tetha) --> Fx = - m.go.x/R
Et F(x) = m.d²x/dt²
--> d²x/dt² = - go.x/R
Equation différentielle du mouvement (direction de l'axe des x) : d²x/dt² + go.x/R = 0
-----
1b)
Composante de F suivant la direction de Oy : Fy = |F|.cos(theta) = m.go.r/R * cos(theta)
...
Réaction du tunnel sur le train : R = -F(y)
...
-----
Sauf distraction. 
Salut,
Ton exercice s'apparente à la première partie de cet exercice de détente que j'avais posté à l'époque (clique sur la maison) :
![]() Coll et J-P partent à l'aventure !
Coll et J-P partent à l'aventure !




