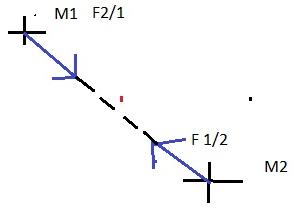
C'est la loi de gravitation donc si tes masses sont la terre et la lune ou la terre et un satellite, oui il faut tenir compte de ces forces, c'est même primordial.
Mais si tes masses sont une pomme et une orange, tu peux te contenter de représenter leur poids (qui est l'attraction terrestre donc l'interaction dont tu parles entre la terre  et les deux objets) mais tu peux négliger l'interaction entre la pomme et l'orange.
Donc réponse : toujours présentes pour deux points matériels ? oui mais souvent négligeable si les masses des deux points matériels sont faibles.

Merci beaucoup pour ta réponse !

Tant qu'on y est il y a un autre point que je  ne comprend pas  (le contexte est le même)
On s'interrese à l'expression de l'energie cinétique dans le réferentiel barycentrique.
On a  Ec=(1/2)m₁v₁²+(1/2)m₂v₂²   jusqu'ici ca va

Mais après on écrit et c'est ceci que je ne vois pas d'où ca vient ??

V₁ = -m₂ /(m₁+m₂)*d(M₁M₂)dt

M1M2,V1,V2 vecteurs

ils ont dû d'abord écrire
(avec le vecteur position du centre de masse)

Puis on dérive par rapport au temps et ça donne l'équation que tu as écrite (car le centre de masse étant immobile, sa dérivée =0) Voir