Inscription / Connexion Nouveau Sujet
Triphasé
 philou28
philou28Bonjour à tous
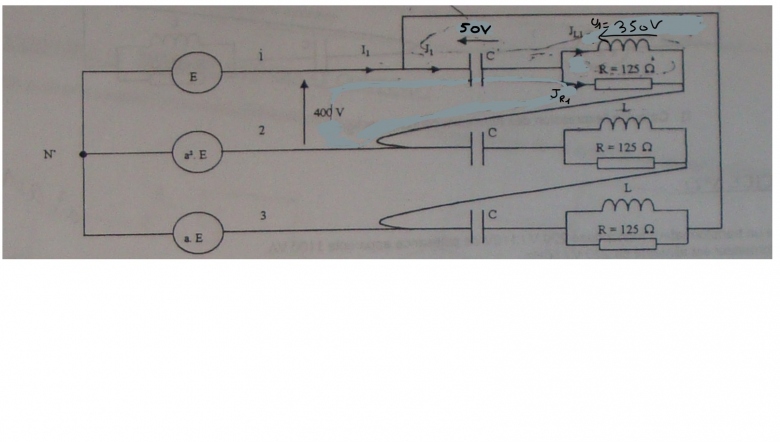
Dans le problème suivant on me demande de trouver les formules complexes de JR1, JL1, J1 et I1.
Voici les données :
J1 en avance de 30° sur E
E est choisi comme origine des phases.
J'ai trouvé JR1 = [2,8 ; 0]
Pouvez vous me donner une aide pour les autres courants ?
Merci
Bonjour,
Il doit manquer des renseignements : on a deux inconnues C et L et une donnée la phase de J1. A moins d'interpréter "trouver les formules complexes" comme donner l'expression littérale.
D'autre part les tensions ajoutées sur le schéma ne peuvent être correctes : 350+50 ne fait 400 que si les deux tension sont en phase ce qui n'est pas le cas.
alors les 50V ils étaient données, c'est moi qui est calculé la tension de 350V par la loi des mailles.
Mais il n'y avait que ca dans le sujet d'annale de partiel de ma formation
Ce n'est pas très simple (ou alors je ne suis pas réveillé).
Mais cette fois on a bien deux données pour deux inconnues.
1- Ecrire la tension aux bornes de C : Uc ; le module est connu, il faut trouver l'argument.
1- Ecrire la tension U12 en fonction de Uc (connue) et Uz (Uz étant la tension aux bornes de R//L)
2- En déduire Uz (module, argument) connaissant U12 et Uc
3- JR1 s'en déduit immédiatement
...
D'accord, j'avais deja trouvé JR1
Donc Uc = [50,-90], est-ce cela car la phase d'un condensateur est connue : -90° ?
U12=[400;0]
U12 = UC + UZ donc UZ = U12 - UC = 400-50j = [403/125 ; -7,1
Donc on peut directement trouver JR1 = UZ/ZR = [400/125 ; -7,1]
C'est cela ?
D'accord, j'avais deja trouvé JR1
... mais faux.
U12=[400;0]
C'est une bonne idée pour les calculs de prendre U12 comme référence, mais il ne faudra pas oublier à la fin que la référence c'est E donc V1.
UZ = U12 - UC = 400-50j = [403/125 ; -7,1
c'est en fait UZ = U12 - UC = 400-(-50j) = [403 ; +7,1]
JR1 = UZ/ZR = [400/125 ; -7,1]
C'est en fait JR1 = UZ/ZR = [403/125 ;+7,1]
Pour la suite même méthode sauf que cette fois c'est la loi des noeuds appliquée à R//L.
Oui effectivement si je garde l'origine des phase en V1,
Uc = [50,-90]
U12=[400;30]
U12 = UC + UZ donc UZ = U12 - UC = 346 + 150j-50j = [377 ; 23,4]
Donc : JR1 = UZ/ZR = [377/125 ; 23,4] A
Est-ce correct ?
J'avais bien dit que c'était une bonne idée de prendre U12 pour faire les calculs et à la fin de repasser à la référence V1.
Vous prenez la référence à V1, vous en tenez compte pour U12, mais par pour Uc qui ne vaut pas [50,-90] puisque J1 est déphasé de 30 par rapport à V1, donc il faut tout reprendre.
A mon avis, reprenez votre message 04-10-24 à 15:2 et corrigez le et ne faites le changement d'origine des phases qu'à la toute fin.
Remarque : vous refaites l'erreur -50j à la place de -Uc=-(-50j)=+50j.
Si je comprends bien il faut que j'ajoute 30° à la phase de Uc si je garde V1 comme référence . Soit -90 +30 ?
Bonjour,
Juste pour que je sache :
Les tensions sur les points marqués 1, 2 et 3 sur le schéma sont triphasées, mais comment sait-on quel est le point (2 ou 3) qui est en avance de 120° sur 1 ?
Je vois, me semble-t-il, un "a²" et un "a" dans les générateurs de sorties 2 et 3, et peut-être l'info est-elle là ... mais je n'ai jamais vu ces marquages nulle part ailleurs, je ne les connais pas.
Quelqu'un sait-il ?
Merci pour les réponses éventuelles.
La phase 1 est la référence, donc la 2 est en retard de 120°, et la 3 en avance de 120.
a = e(j2pi/3)
a² = e(-j2pi/3)
a3 = 1
Bonjour
"On n'en a pas besoin, on a juste besoin de sa phase : \frac{J_1}{C\omega}=U_c=50 V"
Comment en déduit la phase des modules ?
On n'en a pas besoin, on a juste besoin de sa phase :
Comment en déduire la phase car avec cette formule on reste en module
Comment en déduire la phase car avec cette formule on reste en module
J'explicite :
Dans laquelle, on voit que pour déterminer


