Inscription / Connexion Nouveau Sujet
Travail d'une force
Bonjour, je suis bloqué à la première question de cette énoncé.
Un pilote et son planeur volent à la vitesse v que l?on supposera constante, et descendent de 2km d?altitude. La finesse du planeur est de 38 (pour 38 unité de distance horizontale, il descend d?une unité verticalement). Le mouvement est rectiligne.
1) calculer le travail des forces de frottements.
2) justifier pourquoi la force des frottements est constante et en déduire sa valeur.
- car la vitesse est constante.
3) le planeur est pris dans une pompe et remonte son altitude à vitesse constante. Estimer le travail de ces courants ascendants.
Nous ne pouvons qu?utiliser la formule du travail d?une force, de l?énergie cinétique, de la puissance P=F.v et le théorème de l?énergie cinétique.
Merci d?avance.
Bonsoir
Et si tu commençais par expliquer ce que tu as été capable de faire et ce qui te bloque ?
Il sera plus facile de t'aider ensuite ?
N'oublie pas de scanner ton schéma anoté
J'ai :
Et
La variation d'énergie cinétique est nulle car v est constante d'où :
Soit
Sauf qu'on a pas la masse et je ne vois pas comment faire autrement.
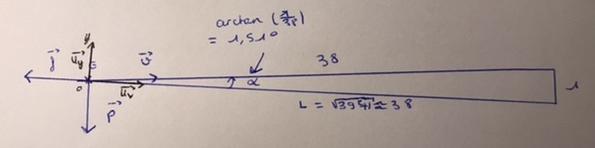
Comme toi, je note la force de traînée (force de frottement). Je note
la force de portance. Comme le mouvement dans le repère terrestre supposé galiléen est rectiligne uniforme :
Comme les trois forces ont le même vecteur déplacement , multiplier par
la relation précédente conduit simplement à une somme des trois travaux nulle :
puisque la force de traînée est perpendiculaire au déplacement, son travail est nul. On obtient donc très simplement :
avec : d=2km. Tu sais depuis longtemps calculer le travail du poids !
Raisonnement analogue ensuite pour la remontée.
Merci !
Mais je ne vois pas ce qu'est la force de portance ni pourquoi vous dites qu'ils ont le même déplacement
La force de portance est la force perpendiculaire à la trajectoire orientée vers le haut ; sans elle, le planeur tomberait !
Le planeur est en mouvement de translation rectiligne uniforme : sur un intervalle de temps donné, tous les points du planeur ont le même vecteur déplacement D.
Remarque : il serait possible (un tout petit peu plus long) de projeter la relation vectorielle sur les deux axes :
projection suivant Ux :
projection suivant Uy :
On obtient ainsi la même expression du travail de la force de frottement.
Donc le travail de la force f est égal à , sauf que nous n'avons pas la masse du planeur pour trouver la valeur du travail.
Énoncé incomplet a priori.
De plus, les questions ne sont pas posées dans un ordre très logique : il faut remarquer que le mouvement est rectiligne uniforme dès la première question...


