Inscription / Connexion Nouveau Sujet
transitoire de RC equa diff
Bonjour
Bon voila j'ai un petit problème sur un exercice de physique ( mais c'est presque plus des maths que de la physique ) et j'arrive pas a trouver quelle erreur j'ai commise
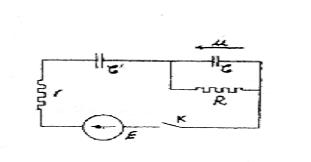
A l'instant initial, les condensateurs C et C', de même capacité C, N'étant pas chargés, on ferme l'interrupteur du circuit
1) Etablir l'equa diff verifiée par la tension u aux bornes de R. On posera 
=2RC et '=rC
Donc j'ai trouvé : d²u/dt² + 2( (1/) + (1/') ) du/dt + u/Rrc = 0
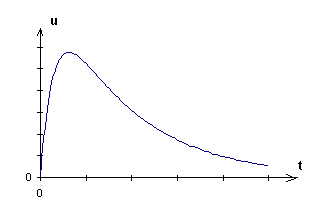
2) Résoudre cette équa diff en supposant r<<R, et donner l'allure de la courbe représentant u(t). Calculer le temps t' au bout duquel u est maximum
Donc j'obtiens une solution de la forme u = e(-t/')[Ae(t/') + Be(-t/')] ou A, B constantes
Mais après je bloque car c pas logique.
Comment faire? Ou ai je fais une erreur?
Merci
Tu aurais du arriver à l'équation différentielle:
d²u/dt² + 2( (1/tau) + (1/tau') ) du/dt + u/RrCC' = 0
d²u/dt² + 2( (1/tau) + (1/tau') ) du/dt + 2u/(tau.tau') = 0
d²u/dt² + 2[(tau+tau')/(tau.tau')] du/dt + 2u/(tau.tau') = 0
soit:
tau.tau'.d²u/dt² + 2.(tau+tau') du/dt + 2u = 0
Si r < < R, on a tau' presque nul -->
2.tau du/dt + 2u = 0
tau. du/dt + u = 0
du/dt + u/tau = 0
u = A.e^(-t/tau)
Et par division capacitive sur la fermeture de K -->
u = (E/2).e^(-t/tau)
-----
Sauf distraction. 
Il n'y a rien de bizarre, c'est même physiquement évident.
Un flanc de tension apparaît sur l'ensemble des 2 condensateurs en série à la fermeture de K (avec r = 0)
Sur ce "flanc", l'impédance de C est très faible devant celle de R. (en effet, pense à i = C.dv/dt avec dv/dt quasi infini à cause du contact considéré comme instantané à la fermeture de K).
Donc au moment du flanc de tension, C et C' se chargent instantanément comme si R n'était pas là.
La tension sur C monte donc instantanément à E/2 (si r = 0 et C = C').
Après un temps infini, la tension sur C redescend à 0, car C' bloque le courant continu et donc R impose une tension nulle sur C.
OK ?
Si r n'est plus négligeable, il faut alors résoudre l'équation:
d²u/dt² + 2[(tau+tau')/(tau.tau')] du/dt + 2u/(tau.tau') = 0
Un exemple, supposons tau = tau', on aurait alors:
d²u/dt² + (4/tau) du/dt + 2u/(tau²) = 0
p = -(2/tau) +/- V((4/tau²) - 2/tau²)
p = (-2 +/- V2)/tau
u = A.e^((-2 - V2).t/tau) + B.e^((-2 + V2).t/tau)
Ici, u(0) = 0 --> A + B = 0
u = B.[e^((-2 + V2).t/tau) - e^((-2 - V2).t/tau)]
On détermine B par E/r = C.du/dt ...
On trouve alors quelque chose comme ceci:
Annuler
connectez vous