Inscription / Connexion Nouveau Sujet
Transformée de Laplace
Bonjour à tous les îlois !
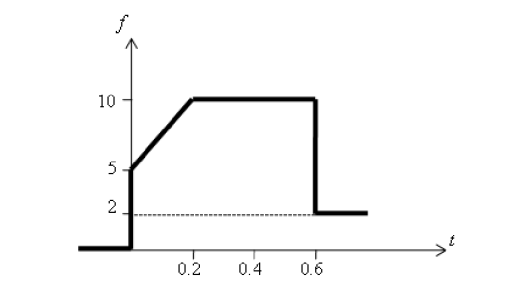
SVP Je voudrais vérifier cet exercice : Déterminer la Transformée de Laplace de la fonction représentée
La TL d'une fonction f(t) est : F(p) = 
de 0 à +
de f(t)exp(-pt) dt
Ce que j'ai fait :
a) Pour t 
]0.6 ; +[ , f(t) = 2 donc F(p) = -2 / p
b) Pour t = 0.6 , f(t) = b avec b ]2 ; 10[ donc je trouve F(p) = -b / p
c) Pour t ]0.2 ; 0.6 [ , f(t) = 10 donc je trouve F(p) = -10 / p
d) Pour t ]5 ; 10[ , f(t) = ax+b je trouve a = 25 et b = 5 donc f(t) = 25t+5 et je trouve F(p) = 20 / p
e) Pour t = 0 , f(t) = 0 donc F(p) = 0
f) Pour t < 0 , f(t) = 0 donc F(p) = 0
Merci de m'aider en vérifiant si tout ce que j'ai écrit est correct ou s'il y'a une autre méthode .
Bonsoir MEV,
Sauf erreur de ma part, c'est de cette façon qu'il faut procéder : 
Laplace
A savoir, décomposer la fonction en une somme de fonctions simples, que tu pourras ensuite transformer dans le domaine de Laplace (en utilisant le théorème du retard).
Mais ça fait plus d'une décennie que je n'ai plus fait ça, peut-être que je me trompe ...
Bonjour SVP , lorsque je trouve les trois fonctions f1 , f2* et f3* je epeux directement appliquer la TL non ?
*** message déplacé ***
J'aimerais savoir si je peux appliquer la TL à chacune de ces fonctions là ensuite sommer les TL ?
Suis-je obligé de passer par le théorème du retard ?
*** message déplacé ***
Bonsoir,
Et si tu commençais par déterminer les fonctions temporelles f1, f2 et f3 pour voir s'il faut introduire un retard pour aboutir à f(t) ?
Bonjour,
Une fonction f_1 qui va de 0 à 0.2
Une fonction f_2 qui va de 0.2 à 0.6
Une fonction f_3 qui va de 0.6 à +∞
f1 est une fonction affine d' ordonée à l'origine 5 et de pente 25
Donc f1 (t)=25t+5.
f2 , est une fonction constante de valeur 10 ainsi pour éviter une discontinuité , il faut annuler la pente de la fonction f_1 pour obtenir une fonction constante.
On construit une fonction f2* en sommant f_2 et la fonction annulant la pente de f_1.
⇒ f2* (t)=10-25t
f3 est la fonction constante de valeur 2 , mais pour trouver f3* je ne sais pas comment je vais faire .
Merci d'avance !!
f3 est la fonction constante de valeur 2 , mais pour trouver f3* je ne sais pas comment je vais faire .
Je propose que f3* = -12 car
f3* = f3+f2-12
Bonsoir,
Je m'inspire de la méthodologie faire précédemment :
Pour ton exercice, on peut décomposer ton signal en trois fonctions :
- Une fonction f1 de 0 à 0,2
- Une fonction de f2 de 0,2 à 0,6
- Une fonction f3 de 0,6 à +inf
==> OK
f1 est une fonction affine d' ordonnée à l'origine 5 et de pente 25
Donc f1: t --> 25t + 5 OK
f2 est une fonction constante, de valeur 10, mais attention, il faut penser à annuler la pente de ta première fonction f1 pour obtenir ta fonction constante, sinon tu ne feras que créer une discontinuité.
On construit f2* en sommant f2 et la fonction annulant la pente de f1 :
f2* = f2 + fonction annulant la pente de f1
on a f2*: t-> 10 - 25t OK
f2 est une fonction constante, de valeur 2. Tu vois sur ton signal qu'il suffit d'ajouter la constante -8 à ton signal d'avant, puisque sa pente est nulle (la fonction f2 juste avant étant constante, pas besoin d'annuler sa pente).
f3*= -8
Tu as maintenant tes trois fonctions élémentaires, tu les passes dans le domaine de Laplace en utilisant le théorème du retard.
Ton signal correspond finalement à F1 + F2 + F3
Annuler
connectez vous