Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence AutreTopics traitant de Autre [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Transformée de Fourier, notations

Posté par
Titana 03-11-17 à 16:51

Bonjour, j'ai quelques soucis avec la compréhension d'une partie de mon cours d'optique qui concerne les transformées de Fourier (TF).

On a défini la TF de f(x) comme \tilde{f}(\nu) = \int_{-\infty}^{+\infty}{f(x)e^{-2i\pi \nu x}dx}.

Plus tard, pour démontrer la propriété de dilatation, nous écrivons : \tilde{(f(\frac{x}{a}))}(\nu) = \int_{-\infty}^{+\infty}{f(\frac{x}{a})e^{-2i\pi \nu x}dx} = \int_{-\infty}^{+\infty}{f(\beta)e^{-2i\pi \nu a\beta}ad\beta}=a \int_{-\infty}^{+\infty}{f(\beta)e^{-2i\pi \nu a\beta}d\beta} = a \tilde{f}(a\nu)

Donc déjà, est-ce qu'en reprenant la notation du 2è paragraphe, on peut écrire :  \tilde{(f(x))}(\nu) = \int_{-\infty}^{+\infty}{f(x)e^{-2i\pi \nu x}dx} ?

Ensuite, j'ai très bien compris le changement de variable \beta=\frac{x}{a} mais, je ne comprends pas trop le résultat car pour moi, a\tilde{f}(a\nu) = a\int_{-\infty}^{+\infty}{f(x)e^{-2i\pi a\nu x}dx} (d'après la première définition)
a \tilde{f}(a\nu) = a\tilde{(f(\beta))}(a\nu) avec \beta = \frac{x}{a} d'où, pour moi a \tilde{f}(a\nu)=a \tilde{(f(\frac{x}{a}))}(a\nu) \neq a\tilde{(f(x))}(a\nu)
Même si on change le nom de la variable ne prenant x pour \beta, pour moi, ce "nouveau" x sera différent de celui d'origine.

Où est-ce que je me trompe dans mon raisonnement ? Quelle information/concept me manque-t-il ?

Merci d'avance pour le temps que vous prendrez afin de m'apporter des réponses et explications !

PS : \tilde{(f(x))}(\nu) signifie que la tilde est sur f(x) et pas uniquement sur le f

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 08:38

Hello

Pour ta première question, soit, mais alors il est plus pertinent d'écrire:

\tilde{f(\frac{x}{a})}(\nu) = ... = a \tilde{f(x)}(a\nu)

Ensuite, la où ça coince:

Citation :
a \tilde{f}(a\nu) = a\tilde{(f(\beta))}(a\nu) avec \beta = \frac{x}{a}
  

Il n'y a pas de changement de variable là dedans. En utilisant ma "précaution" de notation

a \tilde{f}(a\nu) = a\tilde{f(x)}(a\nu) = a\tilde{f(\beta)}(a\nu)

Si toujours pas clair, n'hésite pas, nous reprendrons les bonnes vieilles notations F(\nu)= TF[f(x)] pour bien distinguer les variables.

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 09:59

Oui justement, le problème est que dans mon cours, on n'a pas gardé tout le temps les mêmes notations et ça m'a perdue.. Donc c'est bien ce que j'ai cru comprendre, en fait quand on écrit \tilde{f}(\nu) c'est \tilde{f(x)}(\nu), c'est ça ?

Et donc dans le cours en fait, je pense que quand il s'agissait de x, il écrivait juste \tilde{f}(\nu) mais quand c'était pas x seul, il l'écrivait en "entier"

Citation :
Il n'y a pas de changement de variable là dedans.

C'est cela que j'ai du mal à comprendre. Car dans la démonstration, on utilise = x/a, donc "logiquement", à la fin on devrait avoir a\tilde{f(\beta)}(a\nu) et là, pourquoi le ne serait-il plus égal à x/a ?
Et comme je le disais,
Citation :
Même si on change le nom de la variable en prenant x pour , pour moi, ce "nouveau" x sera différent de celui d'origine.
C'est peut-être ça le fond du problème

Citation :
F(\nu)= TF[f(x)]

Je n'ai vu ces notations que sur internet lors de mes recherches et j'avais eu du mal à les identifier avec celles écrites en cours mais je pense que maintenant, avec ce que vous m'avez dit, j'y arriverai

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 10:59

Citation :
Citation :
Il n'y a pas de changement de variable là dedans.

C'est cela que j'ai du mal à comprendre. Car dans la démonstration, on utilise = x/a, donc "logiquement", à la fin on devrait avoir a\tilde{f(\beta)}(a\nu) et là, pourquoi le ne serait-il plus égal à x/a ?
Et comme je le disais,
Citation :
Même si on change le nom de la variable en prenant x pour , pour moi, ce "nouveau" x sera différent de celui d'origine.
C'est peut-être ça le fond du problème


Ou alors cela est-il dû à la fonction TF elle même ?
Je m'explique : si on prend la fonction f(x)=x² ; on a f(-3)=f(3) alors que -3≠3 ou mieux, pour la fonction
f(x) = 3x ;  f(8) = 24 = 2f(4) et 8/2 = 4 donc f(8)=2×f(8/2).
Et on pourrait dire f(x)=2×f(x/2)

Est ce le même principe avec la TF ?

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 12:45

Attention!   f(x) et f(x/a) sont 2 fonctions différentes: il faut voir f(x/a) comme une fonction composée   (f o g)(x)   où g(x) = x/a

Essaie de reprendre le raisonnement en ayant cela en tête.  Je m'en vais faire une lecture attentive de ce que tu écris pour essayer de "décoincer"

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 14:46

Alors

1) Oublie les analogies avec f(x) = x^2 et  f(x) = 3x, cela finirait de t'embrouiller les idées je le crains

2) Essayons autrement:

Proposition: La transformée de Fourier de la fonction f de la variable x, est la fonction F de la variable :

Notation abrégée de cette proposition: TF (f(x) ) = F()

Soit alors g(x) = f(x/a),  calculons TF(g(x)), que nous noterons G()

TF(f(\frac{x}{a})) = TF(g(x)) = G(\nu) =  \int_{-\infty}^{+\infty}{g(x)e^{-2i\pi \nu x}dx} =  \int_{-\infty}^{+\infty}{f(\frac{x}{a})e^{-2i\pi \nu x}dx}

Or   \int_{-\infty}^{+\infty}{f(\frac{x}{a})e^{-2i\pi \nu x}dx} =  a\int_{-\infty}^{+\infty}{f(\beta)e^{-2i\pi a\nu \beta}d\beta} = aF(a\nu)

Donc   TF(f(\frac{x}{a})) = TF(g(x)) = G(\nu) = aF(a\nu)

Cette syntaxe a sans doute l'avantage de mettre plus facilement des mots devant les expressions et donc de faciliter l'assimilation

Pour faire maintenant le lien avec celle de ton cours:

\tilde{f} = F(\nu)
\tilde{f(\frac{x}{a})} = G(\nu)

J'espère que tu comprends mieux maintenant que lorsque tu poses:

Citation :
a \tilde{f}(a\nu) = a\tilde{(f(\beta))}(a\nu) avec \beta = \frac{x}{a}


il n'y a pas de "changement de variable" car les fonctions "tilde" sont des fonctions de la variable

Et pour tout de même rester sur l'île de Physique Chimie, cela signifie "physiquement" qu'à une dilatation de l'échelle des longueurs va correspondre une compression de l'échelle des vecteurs d'onde (ou aussi qu'à une dilatation de l'échelle de temps va correspondre une compression de l'échelle des fréquences)

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 15:03

Tout d'abord merci de votre patience

Donc ce n'est pas la fonction f qui est appliquée à x dans le 1er cas et à x/a dans le 2e

J'avais pensé à la fonction composée pour la TF...
En fait je crois que le problème c'est la définition de la TF, je n'arrive pas à savoir combien elle a de variables..c'est une fonction à une ou 2 variables ? Car j'ai l'impression qu'il y en a 2 (x et ) mais je suis sûre qu'en réalité il n'y en a qu'une (mais je ne sais pas laquelle des deux). Pourrait-on écrire la TF sous forme de fonction composée (pour éviter d'avoir x et en variables) ?

Merci

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 15:22

La variable de la TF est pas x donc il n'y a pas de changement de varible quand on passe de x/a à x puisque x n'est pas une variable du point de vue de la TF. C'est déjà beaucoup plus clair, merci !

Cependant, je bloque encore, je voulais ré-écrire aF(a) avec la notation TF(f(x)), mais je n'arrive pas à comprendre si aF(a) = aTF(af(x)) ou aTF(f(ax))...
C'est la dernière égalité de la démo qui coince en réalité

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 15:28

Et physiquement, j'avais "compris" mais un autre énorme problème que j'ai c'est que je n'arrive pas à me représenter les choses physiquement. Par exemple, si j'ai bien compris, la TF est la "formule" qui représente la figure obtenue sur l'écran (par exemple avec des fentes ; par diffraction) mais si on me le dit pas, jamais j'arrive à le savoir. Je ne fais pas la relation entre les maths (formules) et la physique, le réel

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 15:28

Citation :
Donc ce n'est pas la fonction f qui est appliquée à x dans le 1er cas et à x/a dans le 2e  


Si!

Mais si la fonction   x \longmapsto f(x) est bien la fonction f,   la fonction   x \longmapsto f(\frac{x}{a}) n'est PAS la fonction f

Citation :
En fait je crois que le problème c'est la définition de la TF, je n'arrive pas à savoir combien elle a de variables....


  je pensais que ce que j'écrivais plus haut me semblait pourtant limpide:

"La transformée de Fourier de la fonction f de la variable x, est la fonction F de la variable "

PS: on parlera de la transformée de Fourier de plusieurs variables si tu le souhaites... mais alors uniquement lorsque tu auras compris la TF de fonctions d'une seule variable ...

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 15:44

Ah mais oui d'accord, j'avais mal compris

J'avais rédigé le 1er messageavant de voir le vôtre, du coup, comme je l'ai mis dans celui d'après, j'ai bien compris que la TF avait 1 seule variable et que c'etait .

Citation :
donc il n'y a pas de changement de varible quand on passe de x/a à x puisque x n'est pas une variable du point de vue de la TF. C'est déjà beaucoup plus clair, merci !


Et par contre, j'aurai bien aimé savoir si aF(a) = aTF(af(x)) ou aTF(f(ax)) ?
Car c'est la toute denière égalité de la démo qui coince pour moi

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 16:08



Nous avions établi il me semble que:  

TF(f(\frac{x}{a})) = TF(g(x)) = G(\nu) = aF(a\nu)  

Donc proposer:  aF(a) = aTF(af(x)) ou aTF(f(ax)) est rageant car introduit un gros doute sur mes qualités pédagogiques ...

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 16:43

Non non, c'est moi qui ne réfléchis pas assez (ou raisonne mal)

J'avais du mal avecla dernière égalité {\color{red}a}\int_{-\infty}^{+\infty}{f({\color{blue}\beta})e^{-2i\pi {\color{red}a\nu }{\color{blue}\beta}}d{\color{blue}\beta}} = {\color{red}a}F({\color{red}a\nu})  . Mais je pense (j'espère) qu'à force de relire, j'ai compris. En fait, on se fiche que ce soit x, , x/a ou , ce qui compte c'est ce que j'ai mis en rouge, juste ? Après tant que la fonction f possède la même variable que celle du d (de l'intégrale) et celle de l'exponentielle, c'est bon (tout ce qui est en bleu). C'est (à peu près) ça ?

Posté par
diracre : Transformée de Fourier, notations 04-11-17 à 17:54

Je vois de la lumière au bout du tunnel

Je crois que tu as bien compris que:

1) dans F(a), la variable c'est a
2) et que dans  F(a\nu) =  \int_{-\infty}^{+\infty}{f(r)e^{-2i\pi a\nu r}dr}  ,  r c'est "juste" une variable d'intégration

Le seul truc qui me chiffonnes dans ce que tu écris c'est le x/a celui la justement on ne s'en fiche pas (c'est tout l'objet de l'exercice, montrer qu'une dilatation su x entraine une compression sur )

Prenons peut être un exemple:

Soit f(x) = e^{-x^2}  la TF correspondante est  F(\nu) = \sqrt{\pi}e^{-\pi^2\nu^2}   (*)

Effectuons une dilatation d'échelle de facteur 2  (a=2)

g(x) = f(\frac{x}{2}) = e^{-(x^2/4}) la TF correspondante est G(\nu) = \sqrt{4\pi}e^{-4\pi^2\nu^2}   (*)

Donc G(\nu) = 2 \times \sqrt{\pi}e^{-\pi^2(2\nu)^2} = .... ... = 2.F(2\nu)  (*)

Donc la transformée de Fourier de f(x/2) est 2F(2)      

On a bon cette fois?  

Transformée de Fourier, notations

Posté par
Titanare : Transformée de Fourier, notations 04-11-17 à 18:36

On peut sortir du tunnel, j'ai compris !

Et j'ai résolu mon problème de départ (qui était écrit sous la forme \tilde {\text{Porte}(\frac{x'}{d})}(\frac{x}{\lambda z}) = d sinc (\frac{\pi dx}{\lambda z}) sachant qu'on avait écrit \tilde{ \text{Porte}(x)}(\nu) = sinc(\pi \nu) du coup, j'ai "corrigé" en mettant \tilde{ \text{Porte}}(\nu) et réussi à retrouver l'égalité. Je vais vérifier toutes les expressions du cours pour les modifier si besoin)

L'exemple confirme bien la propriété

Un grand merci à vous ! Et surtout pour votre patience car j'ai été plus que pénible et longue à la compréhension

Juste, pour terminer, du côté physique, est ce que, comme je le pense (ou plutôt comme j'ai cru le comprendre d'après tout ce qu'on a fait),  la TF est la fonction qui représente la figure obtenue sur un écran (par exemple avec des fentes ; par diffraction)  ? Car j'ai beaucoup de mal avec les représentations physiques : je ne fais pas la relation entre les maths (formules, fonctions) et la physique, le réel

Merci pour tout et désolée de vous embêter encore

Posté par
diracre : Transformée de Fourier, notations 05-11-17 à 07:45

Citation :
la TF est la fonction qui représente la figure obtenue sur un écran


Presque, je dirais qu'elle "permet de représenter"

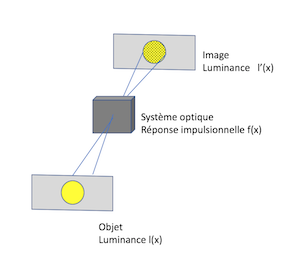
Pour illustrer de manière générale un ças d'utilisation très courant de la TF en optique, un système optique va donner d'une image (caractérisée par sa luminance l(x), x est la position)) une image (caractérisée par sa luminance l'(x) )

On peut alors, sous certaines conditions sur le système optique, introduire une fonction (appelée réponse impulsionnelle,) f(x) telle que:

l'(x) = l(x) * f(x)     (* est l'opérateur produit de convolution)
  
En appliquant la transformation de Fourier à cette expression on obtient

L'() = L() x F() ( est la fréquence spatiale)

F() est appelé la fonction de transfert optique du système
et IF()I (son module) est appelée fonction de transfert de modulation

On va comprendre leur intérêt sur un exemple:
Prenons un objet du la luminance varie de manière sinusoïdale de fréquence spatiale 0, la fonction de transfert de modulation vaudra alors

F( = 0) = 1  (le bruit de fond)
F( = 0) = I'/I où I est la valeur moyenne des signaux image et objet

Tu comprends alors que F caractérise la qualité de restitution du contraste du système optique.

Cette modélisation via une fonction de transfert est très largement utilisée dans les système à capteurs d'images

Transformée de Fourier, notations

Posté par
Titanare : Transformée de Fourier, notations 05-11-17 à 12:44

Oui, d'accord, je vois Tout s'éclaircit

Merci pour tout, j'ai fait un énorme bond en avant grâce à vous

Posté par
diracre : Transformée de Fourier, notations 05-11-17 à 13:57

Parfait! On peut donc pour terminer revenir sur:

Citation :
PS: on parlera de la transformée de Fourier de plusieurs variables si tu le souhaites... mais alors uniquement lorsque tu auras compris la TF de fonctions d'une seule variable


La transformée de Fourier de plusieurs variables, c'est tout simple maintenant:

Tu remplaces x  par  (x1, x2, ...., xn) (coordonnées de la position par exemple)
Et
  par  (1, 2, ...., n) (composantes de la fréquence spatiale par exemple)

Dans l'expression intégrale de la TF:

- l'intégrale simple sur x devient une intégrale multiple sur les composantes x1, ..., xn
- la multiplication x de l'exponentielle devient un produit scalaire:  x11 + ... + xn n

Bon, là on va dire qu'on a fait un premier tour du sujet ...

Posté par
Titanare : Transformée de Fourier, notations 05-11-17 à 15:34

Ah oui d'accord ! Pour le moment, ça n'a pas l'air si terrible que ça en effet


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !