Inscription / Connexion Nouveau Sujet
Transformé de Fourier
Bonjour à tous,
Je me présente quand même ! Je suis Barth, étudiant en deuxième année de mesures physiques, et mon point faible, c'est bien l’électricité. Et voilà un exemple de sujet que je vous présente. Je ne l'ai pas encore fait...
** lien vers l'énoncé effacé **
Mais j'ai bien lu le sujet, et ma première question concerne la question 3 avec Ve (t) = cos(w1t)et Vs(t) qu'il faut donner dans la cas général:
Pour moi, dans le cas général, on a toujours vs(t)= cos(wt) ?
Et pour les cas particulier, je ne vois pas trop ...
Enfin, je vois vraiment pas beaucoup pour le coup !
Merci de pouvoir m'aider ! 
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Bonsoir,
Dans le cas général, on a :
On a :
Pour :
Pour :
Je pense que ça répond à la question...
Pour :
Donc :
Pour :
Pour :
Pour :
Merci !
Alors ce matin, j'ai décidé de faire la première question, et je ne trouve pas:
Pour moi, on a une contre réaction: Donc on a Ve= R/R * Vs
L'autre branche, je dirait que c'est du 1 + pont diviseur ? non ?
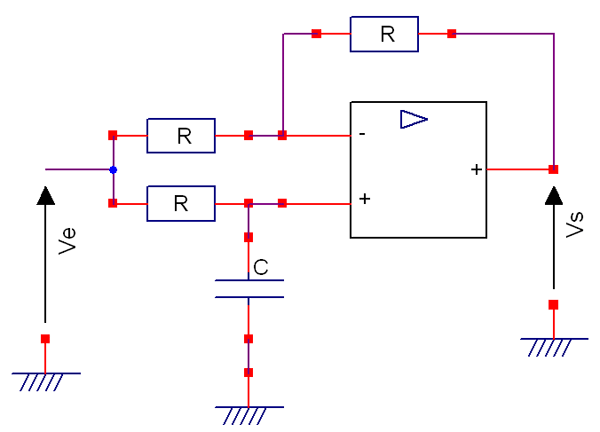
Je n'ai plus le lien mais je me rappelle du schéma...
Le principe est toujours le même. On calcule v+ et on calcule v- (avec Millman de préférence ou pont diviseur dans les cas simples).
Et on fait v+ = v- parce que l'ampli op est considéré comme idéal.
Oui d'accord. Mais j'ai essayé, mais je ne trouve pas du tout ce qu'il faut trouver.
En V+: On utilise aussi Millman ? Ainsi qu'en V- ? Cela doit être le même point dans le circuit ? Ou comme V+=V-, le point choisit est relativement égale à un autre ?
On peut utiliser Millman partout mais, pour v+, le pont diviseur suffit...
On a v+ exprimé en fonction de Ve et v- en fonction de Ve et Vs.
Quand on fait v+ = v-, il ne reste plus que Ve et Vs donc la fonction de transfert.
Je te le ferai mais un peu plus tard. Je n'ai pas le temps maintenant...
Pour autant que je me souvienne du schéma, ce doit être le schéma joint...
(pont diviseur)
(Millman)
Donc :
En posant :
on a :
qui doit être ce qu'on demandait si mes souvenirs sont exacts...
Merci beaucoup ! J'ai essayé de nouveau hier, et j'ai trouvé la même chose que toi ! 
Maintenant, il demande dans la question 4) de trouver taux0 avec T(p) = -p + 1/taux0 / p + taux0 ?
Pour moi, jw = p par rapport à la question 1), donc taux 0 c'est égale à RC ?
Après, dans la question 5)
On veut étudier la réponse indicielle:
a) Écrire l'expression de E(p), transformée de Laplace de l'entrée. ( signal d'entrée qui est Ve(t) = cos(w1t).
La transformée de Laplace pour un cosinus, c'est p² / ( p² + w1² ).
b) Exprimer S(p), transformée de Laplace pour le signal de sortie:
S(p) = T(p)*Ve(p) ?
c) Il faut déterminer la valeur initiale du signal de sortie ? Quel théorème on utilise ?
d) Même question pour un signal d'entrée.
=> Ces deux questions, je ne les comprends pas.
e) Il faut décomposer S(p) en élément simple, je ne l'ai pas encore fait, j'attends juste de savoir si S(p) est bien égale à T(p)*Ve(p) ? Si c'est le cas, je fais le calcul et je le mettrai ici 
Ah oui, la question 6), ce sont les mêmes questions que celle du 5) a) b) e), et je vais pas marquer les mêmes réponses ... Puisque là on étudie un signal rampe.
Encore merci !
Oui, p = j
avec
Pour la réponse indicielle, par définition, en entrée, il faut mettre l'échelon d'Heaviside, pas un cosinus...
On a effectivement :
D accord !
Donc S(p) = T(p)E(p).
a) E(p), le signal d'entrée, c'est égale à u(t). Or une fonction d'échelon est égale à 1/p.
b) Donc S(p)= T(p)*(1/p)
S(p)= (-p+1/ 0/ p + 1/
0/ p + 1/ 0) * (1/p)
0) * (1/p)
S(p)= -p 0 + 1 / p
0 + 1 / p 0 + 1 * (1/p)
0 + 1 * (1/p)
c)J'ai demandé à mon professeur qui m'a répondu, et il faut utiliser le théorème de la valeur initiale:
C'est lim ( p -> + ) = X(p) * p avec X(p) qui est le signal de sortie.
) = X(p) * p avec X(p) qui est le signal de sortie.
Donc, lim (p -> + ) = -p
) = -p 0 +1 / p
0 +1 / p 0 + 1
0 + 1
Et la limite tend vers 1 ? Puisque là, on a de l'infini sur l'infini, forme indéterminée, donc je divise par p le numérateur et dénominateur ?
d) Théorème de la valeur finie, c'est la même chose sauf que p tend vers 0. Donc la limite est 1.
e) Il faut décomposer S(p) en éléments simples:
Donc S(p)= -p 0 + 1 / p( p
0 + 1 / p( p 0 + 1 )
0 + 1 )
En éléments simples:
S(p) = A/p + B/(p 0 + 1) ?
0 + 1) ?
Il n'y a plus qu'à trouver les constantes A et B, mais déjà, es ce bon ?
Pour la question 6) C'est presque la même chose, mais c'est un signal rampe, donc de la forme t.u(t).
a) E(p)= t/p ?
Pour a :
On obtient effectivement :
ou
c)...il faut utiliser le théorème de la valeur initiale :
Oui, effectivement...
Pour d, c'est le théorème de la valeur finale.
Donc :
donc :
Pour e :
Effectivement, la décomposition en éléments simples s'écrit :
Il y a au moins 2 méthodes pour déterminer A et B.
1)
- on multiplie par p et on fait p = 0. On trouve A.
- On multiplie par et on fait
. On trouve B
ou
2)
- L'identification après avoir réduit au même dénominateur.
Pour 6 :
C'est une rampe
Super !  J'ai fais la suite encore
J'ai fais la suite encore 
Pour les coefficients A et B: ( j'utilise la méthode où on multiplie par p et après on fait p = 0 )
A = -1
B = 2
Il faut en déduire dans une question f), l'expression s(t):
Donc on fait la transformée de Laplace inverse: ( on utilise ce que l'on a trouvé dans la question précédente )
Donc s(t)= -u(t) + 2 exp(-t/ 0) ?
0) ?
En petit g) de la question 5), il faut retrouver les valeurs initiale et finale:
Pour finale, il faut faire lim ( t -> 0 ): u(t) + 2 = 1
Pour initiale: lim ( t -> + ): 2exp(-t/
): 2exp(-t/ 0) = 0 donc il reste juste -u(t) = -1.
0) = 0 donc il reste juste -u(t) = -1.
Pour la question 6)
a) E(p) = 1/p² comme vous/tu l'avez/as dit ! 
b) S(p) = T(p)E(p) = T(p)*(1/p²) ( presque la même expression que la question 5).
c) Il faut décomposer de nouveau en éléments simples:
S(p) = A/p² + B/(p+1/ 0) et je crois que l'on rajoute un C/p ?
0) et je crois que l'on rajoute un C/p ?
Ah oui en effet, c'est bien A=1 et B=-2.
Alors pour la 6)
A = 1
C = 2 0
0
B = Il faut dériver. Donc en dérivant j'arrive à : (-2/ 0)/(p+1/
0)/(p+1/ 0)² et je trouve -2
0)² et je trouve -2 0 avec p=0.
0 avec p=0.
Avec A = 1 et B = -2, on retrouve les valeurs initiale et finale trouvées précédemment.
Pour la 6, on a effectivement :
Là, il est presque plus simple d'utiliser l'identification...
même si ce n'est pas appliqué rigoureusement par tout le monde...
Mais, s'il y en a un qui te vouvoie, il est logique d'en faire autant...
Merci beaucoup ! Oui, c'est vrai, aucun problème alors ! 
Serait-il possible que tu m'aides pour un autre devoir sur le même sujet ? Puisque c'est la corrélation qui est demandé.
J'ouvre un autre topic !
Et je te remercie vraiment ! 


