Inscription / Connexion Nouveau Sujet
Transformations du cycle de Carnot
Bonjour à tous,
Je viens à vous suite à une question sur laquelle j'ai bloqué récemment dans un DM, et qui me triture l'esprit.
Il était demandé de justifier qualitativement qu'un cycle de Carnot est composé de 2 adiabatiques réversibles et de 2 isothermes.
J'ai raisonné sur le fait que le cycle de Carnot est un cycle réversible, et que donc l'entropie de création est nulle, mais je n'arrive pas à aboutir à cause des isothermes ou il y a de la chaleur échangée. Il parait que le lien entre la réversibilité et la présence des transformations suscitées est évident, mais je ne vois pas pourquoi.
Je cite la correction du DM : "Réversibilité implique l'égalité de la température du système et de celle de la source lors des transferts thermiques, donc le cycle de Carnot est d'isothermes et d'adiabatiques réversibles"
Merci d'avance à celui ou celle qui prendra 2 minutes pour me répondre 
Thomas
Bonjour,
Tout d'abord une petite clarification : sur une cycle, réversible ou irréversible, le variation d'entropie est nulle. Donc, sur un cycle qui comporte des portions irréversibles, la création d'entropie est positive et donc l'entropie échangée est négative. Je pense que vous savez déjà tout cela, mais je préfère le rapeller.
Maintenant, la définition de la variation d'entropie au cours d'une transformation quelconque est avec
, l'entropie échangée,
étant la température sur la frontière du système étudié, et
l'entropie crée.
Sachant cela, sachant que et sachant que l'on veut
que peut-on en déduire sur
?
Ma "philosophie" est de vous amener à réfléchir et à trouver par vous même, parce que je sais que c'est la seule façon pour que vous compreniez et reteniez. Evidemment, cela demande plus d'effort de votre part et de ma part que si je vous balançait la solution en ajoutant "recopier sans comprendre ne sert à rien" pour vous et me donner bonne conscience.
Bonne soirée.
Tout d'abord merci de m'aider ! Voila ce que j'ai obtenu au brouillon :
Ayant 
S = Sr + Sc, et que on a S = 0 sur le cycle et que l'on veut Sc = 0, il vient que Sr doit être égal à 0 aussi.
Après, il faut (je suppose) montrer que seules les isothermes remplissent cette condition. Pour ça, j'ai supposé que la transformation était quelconque, on a donc
Qe = dU - W = Cv.dT +P.dV
Il vient ensuite Se = 
Qc/Tc + Qf/Tf
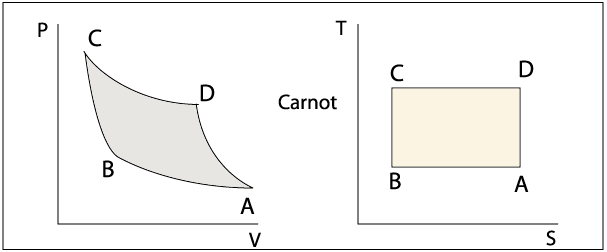
où les intégrales se font respectivement sur les branches du cycles où le système est au contact des sources chaude puis froide (càd CD et AB sur l'image ci-jointe)
En supposant maintenant que ces branches sont des isothermes, Cv.dT devient nul et on en déduis après intégration que
Se = nR.(Tf.ln(Vb/Va) + Tc.ln(Vd/Vc))
Mais après je ne vois pas comment aboutir. J'ai pensé aux lois de Laplace mais je n'arrive pas à m'y ramener.
De plus, j'ai fait l'hypothèse que les branches étaient isothermes, mais je ne montre pas que seules les isothermes sont solutions au problème, n'est-ce pas ?
Thomas
PS : Excusez moi si mes lignes ne sont pas très lisible mais je n'ai pas trouvé comment faire la division dans la barre d'outils mathématiques ^^
Annuler
connectez vous