Inscription / Connexion Nouveau Sujet
Trajectoire en coordonnées polaires
Bonjour, je bloque à un exercice...
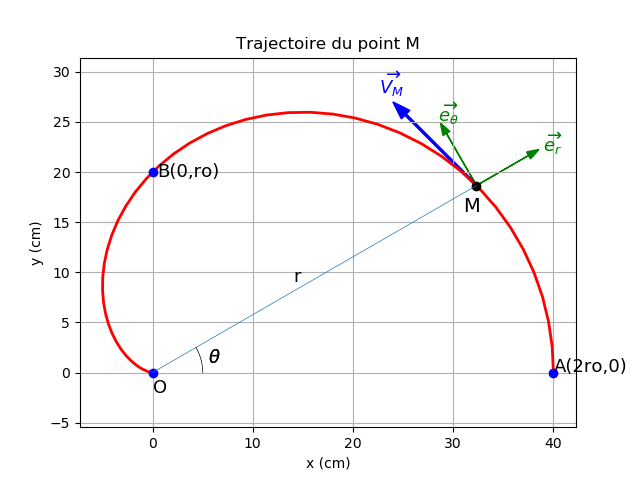
Un point matériel M décrit la trajectoire plane dont l'équation s'écrit, en coordonnées polaires : r(t)=r0(1+cosθ(t)) avec r0=20cm e tθ∈[0,π]
De plus, θ'=ω0, avecω0 une constante positive.
1 .Tracer l'allure de la trajectoire à l'aide de quelques points particuliers.
La trajectoire dépend-elle de la loi horaire de θ?
2 .Déterminer les composantes de la vitesse dans la base polaire. Placer le vecteur vitesse en quelques points caractéristiques de la courbe.
3 .En déduire la longueur de la trajectoire et faire l'application numérique.
4 .Déterminer les composantes de l'accélération.
1.La trajectoire dépend de la loi horaire de θ.
2.v(t) = r'er + rer
= -roω0sinθ(t)er + reω0eθ
= rp((-ω0sinθ(t))er + (ω0 + ω0cosθ(t)))eθ
3. Pour cette question je ne vois pas comment déduire la longueur de la trajectoire...
Bonjour
L'équation polaire de la trajectoire est r=f(
) et ne dépend donc pas de la loi =f(t)Je comprends pas la différence
Pour la question 3 : il faut d'abord calculer la norme V(t) du vecteur vitesse. Indication : il y a des simplifications en passant à l'angle moitié :
un déplacement élémentaire le long de la trajectoire entre les instants de dates t et (t+dt) peux s'écrire : ds=V(t).dt
La longueur de la demie cardioïde de A à O s'écrit donc :
en posant tA=0 (instant de départ en A, que vaut l'instant tO d'arrivée en O ?
=
o.t
A la date t= 0, le point mobile M est en A : =0 ;
Le point mobile M est en O pour =
rad ; donc tO = ?
Tu as raison mais, comme je l'ai fait dans mon précédent message, il est tout à fait possible de choisir l'instant initial au passage en A de sorte que =0 si t=0. Cela permet d'obtenir une constante C1 nulle.
=o.t
A la date t= 0, le point mobile M est en A :
=0 ;
Le point mobile M est en O pour
=rad ; donc tO = ?C'est une constante définie dans l'énoncé. Sa valeur numérique n'est pas donnée car tu vas démontrer que la longueur de la branche de cardioïde entre A et O ne dépend que de la valeur de ro .
C'est la longueur de la courbe entre A et O qui est demandée (longueur de la courbe tracée en rouge), pas la distance entre ces deux points.
Commence par exprimer la norme du vecteur vitesse que j'ai notée V(t). Seul le calcul littéral est demandée. Ensuite, tu considères que la distance parcourue entre t et (t+dt) le long de la trajectoire en rouge sur le schéma est : ds=V(t).dt. Reste alors à intégrer sur la durée totale du parcours comme déjà expliqué. Les calculs littéraux intermédiaires font intervenir t, o, ro. Le résultat final fait intervenir uniquement ro.
Je t'aide un peu pour démarrer cette dernière question, nettement plus difficile que tous les autres exercices que tu as proposés sur ce forum... Tu as déjà démontré les expressions des composantes radiale et tangentielle de la vitesse :
La norme du vecteur vitesse est ainsi :
Je te laisse continuer... N'oublie pas de tenir compte de mon message du 21-09-20 à 19:33...
Annuler
connectez vous