Inscription / Connexion Nouveau Sujet
Trajectoire avion
Bonjour, j'ai un problème de physique à résoudre et je trouve un résultat assez dérangeant.
Voici mon énoncé:
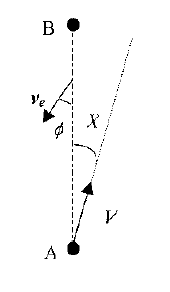
On considère le sol comme un référentiel galiléen (référentiel absolu) noté R. Un avion doit se déplacer en ligne droite d'un point A vers un point au sol B. Il subit un vent contraire de vitesse ve. le vecteur  e fait un angle
e fait un angle  avec la trajectoire AB. L'avion vole à une vitesse constante V par rapport à l'air. Cette vitesse fait un angle X avec la route au sol AB.
avec la trajectoire AB. L'avion vole à une vitesse constante V par rapport à l'air. Cette vitesse fait un angle X avec la route au sol AB.
Voici un lien de l'énoncé où on le peut voir très clairement le schéma :
Les questions qui me sont posées sont:
1a) Calculer la vitesse  a de l'avion dans le réferentiel R en fonction des données.
a de l'avion dans le réferentiel R en fonction des données.
Pour cette première question j'ai utilisé la formule de la compostion des vitesses et je l'ai ensuite appliquer pour mon cas :
Formule: a=
a= r +
r + e
e
Donc Référentiel absolu : Terre Référentiel relatif: l'avion
J'ai utiliser une base cartésienne (x,y,z) avec y en ordonnée et x en abscisse.
J'obtient : va= V cos(X) + ve
cos(X) + ve cos(
cos( ) (portée sur l'axe y).
) (portée sur l'axe y).
c) Calculer l'angle de correction X que le pilote doit afficher dans le cas où V=445 km/h pour onctrer un vent de vitesse ve=56 km/h et  =20°
=20°
je trouve un angle X=83°. Cela me semble un poil trop grand pour que cela soit possible 
Sinon apres j'ai également la question 3 a faire mais si quelqu'un voit mon erreur je pourrai apres bien avancer
Merci
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Pour que la trajectoire soit une ligne droite, il faut que la vitesse de l'avion dans le repère n'ait pas de composante horizontale.
Tu t'es trompé dans la projection.
Si je définie la trajectoire AB comme axe d'ordonnée y , je ne devrais avoir qu'une composante sur y , tel que :
ve: vitesse du vent contraire : ve  cos
cos 
v: vitesse de l'avion par rapport a l'air : v cos X
cos X
non?
PS: Merci de l'edit 
Absolument, ce qui te permet de calculer la vitesse de l'avion par rapport au repère .
Mais ça ne te donne pas de condition permettant de déterminer .
Oui, merci donaldo t'avais raison. Puisque pour déterminer mon angle de correction j'ai besoin d'une deuxieme équation car j'ai deux inconnues.
En projettant sur X, j'obtiens :ve= ve sin(
sin(
et v=v sinX
sinX
Système de deux équations a deux inconnues:
va= ve cos
cos + v
+ v cosX
cosX
va= ve sin
sin + v
+ v sinX
sinX
Je pense que c'est cela 
Merci de m'avoir éguiller 
C'est "presque" ça.
En reprenant tes notations:
(note le signe négatif, la vitesse relative de l'avion et la vitesse du vent ont des directions opposées)
La condition suffit à déterminer la valeur de l'angle
.
Oui , merci je trouve un angle de 2,45° et une vitesse de l'avion de 400km/h , plutôt faisable.
J'aurai une dernière question a poser au sujet de cet exercice :
En B, l'avion arrive au-dessus d'une balise au sol à une date prise pour origine des temps. Le contrôleur demande alors au pilote de réaliser à altitude constante un circuit d'attente BCDE constitué de deux parties semi-circulaires BC et DE et de deux parties rectilignes CD et EB. II lui indique à quelle date tB l'avion doit se présenter à nouveau
au-dessus de la balise B
Le pilote adapte l'inclinaison de l'appareil et donc le rayon des tronçons semi- circulaires BC et DE de manière à ce que ceux-ci durent 1 minute chacun. Durant cette attente, la vitesse V de l'avion est supposée constante et égale à 222 km.h"1, tandis que la vitesse du vent est toujours ve = 56 km.h"1, et  =20°.
=20°.
A quelle date tv le pilote doit-il entreprendre le virage DE si la date de passage au dessus du point B, imposée par le contrôleur, est tB = 4 minutes ?
Pour cette question on me dit que les tronçons des semis-circulaires correspond à 1 minute
Pour les tronçons des deux rectilignes je suis partit des équations de départ :
Va=V+Ve avec les projections sur X et Y :
Vay= Vx cosX - Ve
cosX - Ve cos
cos
Vax= Vx sinX - Ve
sinX - Ve sin
sin
j'ai décider ensuite de les intégrer par la variable t (temps) :
Y= Vx cosX
cosX t - Ve
t - Ve cos
cos
 t + constante
t + constante
X= Vx sinX
sinX t - Ve
t - Ve sin
sin
 t + constante
t + constante
X et Y repésentent les distances
Je pense qu'il faut que je garde la condition Vax=0 pour que l'avion vole droit, mais ce qui me gêne est plutot la constante , car je n'ai pas de condition pour la supprimée
Remarque : pour le tronçon de CD on a la vitesse du vent et la vitesse de l'avion dans le même sens. Donc on aura un changement de signe.
Merci
Vérifier simplement que, à vitesse relative égale, l'angle de correction doit être identique sur le tronçon CD et le tronçon EB.
Calcule-le comme à la question précédente pour en déduire la vitesse de l'avion dans le repère fixe sachant que la vitesse du vent se soustrait à la vitesse relative de l'avion sur le tronçon BE et s'y rajoute sur le tronçon CD.
Connaissant la vitesse de l'avion sur les deux tronçons, tu en déduiras facilement le temps mis par celui-ci pour les parcourir.
Oui, tu as raison j'ai bien recalculer les vitesses des deux tronçons. Voici ce que j'obtiens
Pour le tronçon EB :
Vay=Vx cos(X)-Ve
cos(X)-Ve cos
cos
Vax=Vx sin(X)-Ve
sin(X)-Ve sin
sin
Or condition ligne droite : Vax=0.
J'obtiens donc un angle de correction X= 4,94° et une vitesse Vay=169km/h
Pour le tronçon CD :
Vay=Vx cos(X)+Ve
cos(X)+Ve cos
cos
Vax=Vx sin(X)+Ve
sin(X)+Ve sin
sin
Or condition ligne droite : Vax=0.
J'obtiens donc un angle de correction X= -4,94° et une vitesse Vay=273km/h
On me dit : "la date de passage au dessus du point B, imposée par le contrôleur, est tB= 4min"
Donc sur le tronçon EB, on a tB= 4min , soit arrivée a la balise B en 4min.
V=d/t : avec Vay= 169km/h et t= 4 j'obtiens d= 676m
Pour le tronçon BC : tc= 1min
Pour le tronçon CD : on a la longueur EB=CD=676m et Vay=273 km/h
Donc td= 2,4 min
Et le tronçon DE : te= 1 min
Voici ce que j'obtiens
Cela ne te fait pas tiquer que d'après tes réponses, l'avion vole moins vite avec le vent dans le dos qu'avec le vent de face ?
Trajet AB
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) - Ve.cos(Phi)
V = 445, Ve = 56 et Phi = 20° -->
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) - Ve.cos(Phi)
445.sin(X) - 56.sin(20°) = 0
Va = 445.cos(20°) - Ve.cos(Phi)
sin(X) = 56.sin(20°)/445 = 0,04304...
X = 2,47°
---> cos(X) = racine(1 - 0,04304²) = 0,998147...
Va = V.cos(X) - Ve.cos(Phi)
Va = 445*0,998147- 45*cos(20°)
Va = 402 km/h
----------
Trajet CD
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) + Ve.cos(Phi)
X = 2,47°
Va = 445*0,998147 + 45*cos(20°)
Va = 486 km/h
----------
Sauf distraction. 
L'énoncé précise que la durée tB correspond au temps où l'avion doit se présenter à la balise B. On ne précise qu'il doit arriver dans 4 min à la balise B.
J-P je suis tout a fait d'accord avec tes résultats.
Pour la prémière question que j'avais posé je trouvais bien un angle de correction de X=2,47 et une vitesse de Va= 400km/h.
Par contre pour le trajet CD (question d'après) la vitesse V n'est plus égale a 445km/h mais a 222km/h avec toujours le vitesse du vent de 56km/h
alors je trouve Va= 273km/h pour le tronçon CD et Va= 169 km/h pour le tronçon EB.
Donc avec vent dans le dos je vole bien plus vite.

On dit aussi que la référence des temps est prise à l'instant ou l'avion passe pour la première fois au point B. Ne faut-il pas en conclure que le circuit d'attente entier doit être parcouru en 4 minutes?
Y a-t-il d'autres questions après?
PS: , d'accord, mais attention tout de même aux unités dans tes calculs...
Je suis d'accord avec toi donaldos il doit bien de retrouver au point B à nouveau dans 4 min.
Mais lorsqu'il arrive au point B qui est également l'origine des temps c'est à t=0.
Si cela est bien le temps total parcouru: Ttotal= 4min
Et Ttotal= tEB + tBC + tCD + tDE . Or tBc et tDE sont égales à 1 min
J'obtiens comme équation : 2= tEB + tBC
Or tEb= EB/Vay1 = EB/169 et tBC= BC/Vay2 = BC/273. Voila ce que j'en pense
Merci
Pendant la boucle :
Avec V = 222 km/h
Trajet AB
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) - Ve.cos(Phi)
V = 222, Ve = 56 et Phi = 20° -->
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) - Ve.cos(Phi)
222.sin(X) - 56.sin(20°) = 0
Va = 222.cos(20°) - Ve.cos(Phi)
sin(X) = 56.sin(20°)/222= 0,08627...
X = 4,95°
---> cos(X) = racine(1 - 0,08627²) = 0,996262...
Va = V.cos(X) - Ve.cos(Phi)
Va = 222*0,996262- 56*cos(20°)
Va = 169 km/h
----------
Trajet CD
V.sin(X) - Ve.sin(Phi) = 0
Va = V.cos(X) + Ve.cos(Phi)
X = 4,95°
Va = 222*0,996362- 56*cos(20°)
Va = 274 km/h
----------
durée trajet AB : t1 = AB/169
durée trajet CD : t2 = AB/274
durée de ces 2 trajets = 2min = 1/30 h
AB/169 + AB/274 = 1/30
AB = 3,48 km
durée du trajet AB = 0,0206 h = 1 min 14s arrondi
durée du trajet CD = 0,0127 h = 0 min 46s arrondi
1ere date du passage en D = 1 min 46s
-----
Aux erreurs près. 


