Inscription / Connexion Nouveau Sujet
Trajectoire
Bonsoir et merci déjà pour l'attention apporté à mon message.
J'ai rencontré des difficultés avec l'exercice suivant :
Dans un repère cartésien orthonormé (O,i,j,k) du plan xOy, on considère une particule M en mouvement selon les équations horaires : x(t) = axos(wt), y(t) = bcos(wt -  ), a,b positifs et 0<
), a,b positifs et 0< <
<  . Déterminer l'équation de la trajectoire de M ainsi que sa nature suivant les valeurs de
. Déterminer l'équation de la trajectoire de M ainsi que sa nature suivant les valeurs de  .
.
Merci d'avance
Bonjour
Méthode possible : développer le second cosinus puis remarquer que la somme sinus carré plus cosinus carré vaut 1.
Déjà fait
Bonjour
Méthode possible : développer le second cosinus puis remarquer que la somme sinus carré plus cosinus carré vaut 1.
x²/a² + y²/b² -2xycos(
 )/ab = sin²
)/ab = sin²
Mais donner la nature et caractériser c'est ça mon problème.
Remarque : es-tu bien sûr que les cas particuliers
 =0 et
=0 et  =
= sont ici hors sujet ?
sont ici hors sujet ?Merci déjà.
Pour l'inégalité elle est bien stricte
Dommage car ces cas particuliers sont intéressants et ont des applications pratiques (méthode de Lissajoux en électricité par exemple).
Pour revenir à ton exercice : ton équation cartésienne de la trajectoire est correcte. La trajectoire est une ellipse inscrite dans un rectangle de largeur 2a et de hauteur 2b puisque chaque cosinus varie entre -1 et 1.
Tu dois savoir que, lorsque les axes de symétrie de l'ellipse se confondent avec les axes du repère, l'équation cartésienne de l'ellipse s'écrit :
Imagine que tu fasses tourner les axes de symétrie de cette ellipse d'un angle
 ; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) :
; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) : Tu pourras aussi envisager les trois cas :
 <
< /2
/2
 =
= /2
/2
 >
> /2
/2
Cela n'est peut-être pas demandé ici mais il pourrait être intéressant de savoir dans quel sens tourne la particule sur la trajectoire.
Pour l'inégalité elle est bien stricte
Dommage car ces cas particuliers sont intéressants et ont des applications pratiques (méthode de Lissajoux en électricité par exemple).
Pour revenir à ton exercice : ton équation cartésienne de la trajectoire est correcte. La trajectoire est une ellipse inscrite dans un rectangle de largeur 2a et de hauteur 2b puisque chaque cosinus varie entre -1 et 1.
Tu dois savoir que, lorsque les axes de symétrie de l'ellipse se confondent avec les axes du repère, l'équation cartésienne de l'ellipse s'écrit :
Imagine que tu fasses tourner les axes de symétrie de cette ellipse d'un angle
 ; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) :
; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) : Tu pourras aussi envisager les trois cas :
 <
< /2
/2
 =
= /2
/2
 >
> /2
/2
Cela n'est peut-être pas demandé ici mais il pourrait être intéressant de savoir dans quel sens tourne la particule sur la trajectoire.
Merci beaucoup Vanoise pour vos explications et pour votre aide encore merci beaucoup.
teyoteyoteyoteyoteyoteyoteyo
Pour l'inégalité elle est bien stricte
Dommage car ces cas particuliers sont intéressants et ont des applications pratiques (méthode de Lissajoux en électricité par exemple).
Pour revenir à ton exercice : ton équation cartésienne de la trajectoire est correcte. La trajectoire est une ellipse inscrite dans un rectangle de largeur 2a et de hauteur 2b puisque chaque cosinus varie entre -1 et 1.
Tu dois savoir que, lorsque les axes de symétrie de l'ellipse se confondent avec les axes du repère, l'équation cartésienne de l'ellipse s'écrit :
Imagine que tu fasses tourner les axes de symétrie de cette ellipse d'un angle
 ; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) :
; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) : Tu pourras aussi envisager les trois cas :
 <
< /2
/2
 =
= /2
/2
 >
> /2
/2
Cela n'est peut-être pas demandé ici mais il pourrait être intéressant de savoir dans quel sens tourne la particule sur la trajectoire.
S'il vous plait la pourquoi l'ellipse est t-elle inscrite dans un rectangle de longueur 2a et de largeur 2b ?
S'il vous plait la pourquoi l'ellipse est t-elle inscrite dans un rectangle de longueur 2a et de largeur 2b ?
Puisque chaque cosinus varie entre -1 et 1 au cours du temps, x varie entre -a et a et y varie entre -b et b.
teyoteyoteyoteyoteyoteyoteyo
Pour l'inégalité elle est bien stricte
Dommage car ces cas particuliers sont intéressants et ont des applications pratiques (méthode de Lissajoux en électricité par exemple).
Pour revenir à ton exercice : ton équation cartésienne de la trajectoire est correcte. La trajectoire est une ellipse inscrite dans un rectangle de largeur 2a et de hauteur 2b puisque chaque cosinus varie entre -1 et 1.
Tu dois savoir que, lorsque les axes de symétrie de l'ellipse se confondent avec les axes du repère, l'équation cartésienne de l'ellipse s'écrit :
Imagine que tu fasses tourner les axes de symétrie de cette ellipse d'un angle
 ; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) :
; tu obtiens alors une équation cartésienne analogue à celle de cet exercice. Plus de renseignement ici (paragraphe sur l'équation cartésienne en particulier) : Tu pourras aussi envisager les trois cas :
 <
< /2
/2
 =
= /2
/2
 >
> /2
/2
Cela n'est peut-être pas demandé ici mais il pourrait être intéressant de savoir dans quel sens tourne la particule sur la trajectoire.
S'il vous plait la pourquoi l'ellipse est t-elle inscrite dans un rectangle de longueur 2a et de largeur 2b ?
Lorsque je discute suivant les valeurs de
 :
:
pour
 <
<  /2 : x²/a² + y²/b² -2xycos
/2 : x²/a² + y²/b² -2xycos /ab > x²/a² + y²/b²
/ab > x²/a² + y²/b²
pour
 >
>  /2 : x²/a² + y²/b² -2xycos
/2 : x²/a² + y²/b² -2xycos /ab < x²/a² + y²/b²
/ab < x²/a² + y²/b²
Mais à ce niveau j'ai des difficultés à conclure sur la trajectoire.
Je ne pense pas que le concepteur de cet énoncé demande d'expliciter l'angle  entre l'axe (Ox) et le grand axe de l'ellipse (angle évoqué dans mon message du 05-01-20 à 09:54). Simplement en réfléchissant aux signes de y quand x vaut +a puis -a, tu peux assez facilement montrer que :
entre l'axe (Ox) et le grand axe de l'ellipse (angle évoqué dans mon message du 05-01-20 à 09:54). Simplement en réfléchissant aux signes de y quand x vaut +a puis -a, tu peux assez facilement montrer que :
1° le grand axe de l'ellipse a un coefficient directeur positif pour 0< <
< /2
/2
2° le grand axe de l'ellipse a un coefficient directeur négatif pour  /2<
/2< <
<
Tu peux aussi montrer que, dans le cas particulier  =
= /2, les axes de symétrie de l'ellipse sont les axes (Ox et (Oy) puisque l'équation de l'ellipse est alors simplement :
/2, les axes de symétrie de l'ellipse sont les axes (Ox et (Oy) puisque l'équation de l'ellipse est alors simplement :
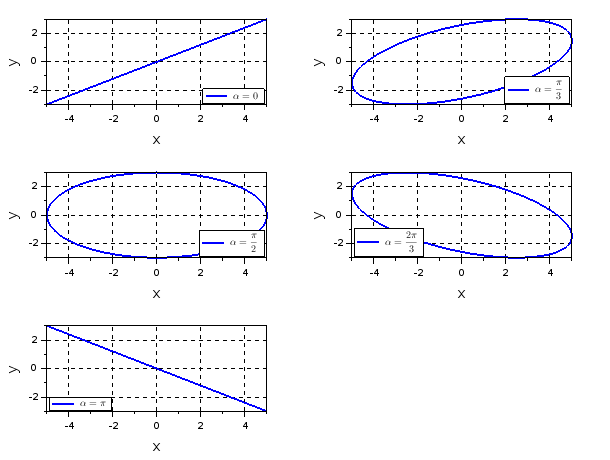
Je t'ai résumé la situation ci-dessous. J'ai rajouté les cas particuliers  =0 et
=0 et  =
= . Ton énoncé n'en parle pas mais de nombreux autres exercices demandent de réfléchir à ces situations. Il est fréquent également de demander le sens de rotation de la particule sur l'ellipse...
. Ton énoncé n'en parle pas mais de nombreux autres exercices demandent de réfléchir à ces situations. Il est fréquent également de demander le sens de rotation de la particule sur l'ellipse...