Inscription / Connexion Nouveau Sujet
trajectoire
Bonsoir,
j'ai un petit probleme pour exprimer ma trajectoire qui est
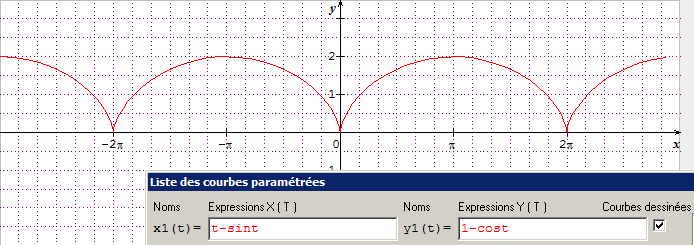
OM (x=R(w.t-sin(wt)) ; y=R(1-cos(wt)) ; z=0)
j'ai tenté diverse transformation, et celle qui me parait la plsu aboutie est :
(2 + (
2=1
Mais après je ne vois pas comment me débarasser de t
J'ai donc entré l'equation parametrique dans am calculatrice pour voir la trajectoire, et j'obtiens une sorte de vague (je crois que ca s'appelle un cycloide), de période 2.R.Pi , avec une tangente verticale a l'origine.
Quelqu'un saurait trouver l'equation de la trajectoire?
merci beaucoup!
sinon, brocoli, un superbe site est celui de Serge Mehl où tu trouveras, ici ![]() un développement sur la roulette, la cycloïde de Pascal :
un développement sur la roulette, la cycloïde de Pascal :
La cycloïde est, par définition, engendrée par un point M de la circonférence d'un cercle roulant sans glisser sur une droite (d)
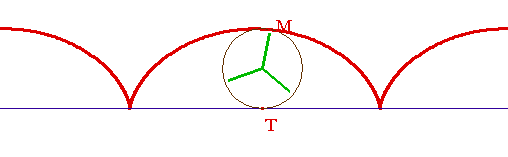
Il suffit d'imaginez une tête de clou plantée dans le pneu d'un vélo : elle ne tourne pas "en rond", elle décrit une cycloïde.
les cycloïdes allongées et raccourcies sont également très sympas...
------------
ce qu'il pourrait être intéressant de chercher, avec tes équations en R, c'est la longueur d'une arche de cycloïde : tu devrais trouver 8R

vraiment intéressant le site!
l'arche de cycloide c'est ce qu'on appelle le rayon curviligne?
Ca ma permis de comprendre pourquoi dans mon cas j'avais une cycloide "normale", car sur le site il y a l'equation des cycloide allongées et raccourcies (qui divergent par un membre en plus).
En gros on a a*t-b*sin(t)
si a=b avec c'est une cycloide normale
si a<b c'est une cycloide allongée
si a>b c'est une cycloide raccourcie
Mais en gros si on veut tracer la trajectoire a la main, on place 3points :
-le 1er lorsque le point est a l'origine,
-puis lorsqu'il est au plus haut (donc on a tourner de Pi*r),
-puis lorsque le point est de nouveau "sur" l'axe des abscisses (on aura tourné au total de 2*Pi*r)
Après il ne reste plus qu'a relier les points ensemble, et voila on a notre cycloide!