Inscription / Connexion Nouveau Sujet
Train dans le référentiel terrestre considéré comme non galiléen
Bonsoir,
Je suis en BTS Topo; J'ai un exercice à faire et je rencontre quelques problèmes…
J'avoue avoir des difficultés sur le cours.
J'en ai une ici, dans une mise en pratique concernant la force de Coriolis.
Voici l'énoncé:
Un train tourne autour de la Terre dans le même sens le long du 45 parallèle.
Calculer la force de Coriolis qu'il subit et la comparer à son poids.
Sa masse m=200t, sa vitesse=200km/h
Il y a en remarque: "Vous devez connaitre les données numérique manquantes"
J'ai rajouté:
Rayon de la Terre= 6400km
g=9,8m/s²
L'expression du poids au 45ᵉ parallèle est : P= mk. M𝗍/(R𝗍²)-mω²rT.cos²𝜸 avec 𝜸=π/4
La deuxième loi dans un référentiel non galiléen est:
F+Fie+Fic=m.aᵣ (en vecteur)
avec:
aᵣ= accélération du train dans le repère mobile (R')
Fie=Force d'inertie d'entrainement=mω².OM ou mω²rT.cos𝜸 avec 𝜸=π/4
Fic=Force d'inertie de Coriolis=2mω⋀Vᵣ avec ω et Vᵣ en vecteur et Vᵣ la vitesse relative du train.
Le vecteur Vᵣ n'a qu'une composante selon z, pas de composantes en x et en y.
Quelles sont les coordonnées d'ω? Ce n'est pas vraiment vecteur, c'est une vitesse angulaire.
Je sais que ω=d
/dt
je sais calculer le produit vectoriel de deux vecteurs u et v mais là... je ne vois pas.
Merci
bonjour,
dans la formule de la force de Coriolis, 
désigne le vecteur "vitesse instantanée de rotation"
= w
avec w: vitesse angulaire, : vecteur unitaire directeur de l'axe (instantané) de rotation
si mes souvenirs de méca du solide sont bons... 
Bonjour krinn,
D'accord, donc il faut simplement multiplier 
par le vecteur unitaire du repère mobile (R').
Les deux vecteurs sont colinéaires et aᵣ , l'accélération relative du train dans le repère mobile (R') est une accélération tangentielle donc nulle vu que sa vitesse est constante...si j'ai bien tout compris.
Ca s'éclaire un peu, je continue.
Merci!
Avec
la force de Coriolis
la vitesse angulaire de rotation de la Terre autour de son axe polaire.
le vecteur vitesse du train par rapport à la Terre.
un vecteur unitaire directeur de l'axe de rotation de la Terre.
On note souvent pour
= 2Pi/(24*3600) rad/s
v = 200/3,6 m/s
et angle fait entre les vecteurs v et e = 90°
...
Sauf distraction. 
Bonjour J-P,
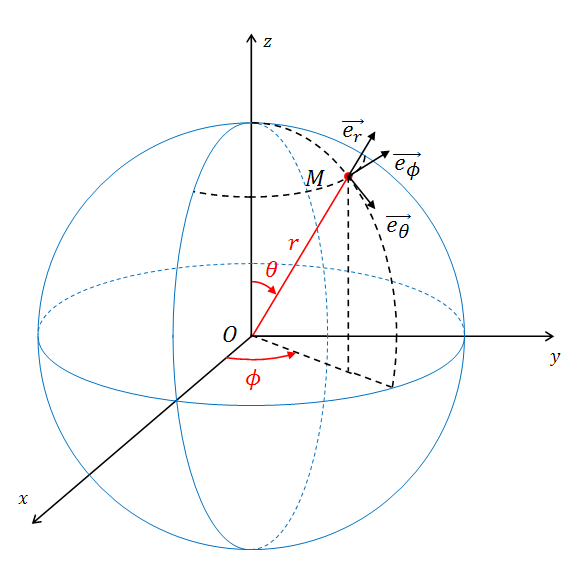
Donc, si j'ai bien tout compris, par rapport au schéma que j'ai joint:
- le vecteur vitesse 
est colinéaire au vecteur e
et le vecteur . est colinéaire à z.
- les vecteurs et . sont donc orthogonaux.
Le produit vectoriel de ces deux vecteurs orthogonaux va donner un vecteur centrifuge sur un plan passant par M et parallèle au plan (O,x,y).
Dans le repère (O,x,y,z), les coordonnées de v.e sont (-v.sin
; v.cos
; 0) et celles de . sont ( 0 ;0 ; ), c'est bien ça?
Et le produit vectoriel (v.e
.) donne (v.cos.+v.sin.j+0) est-ce juste??
Par contre, je ne vois par quand faire intervenir la latitude, est-ce uniquement pour l'expression de la gravité?
Et pour l'angle , quelle mesure faut-il que je prenne? 2π?
Merci
bonjour,
- les vecteurs
et sont donc orthogonaux.et donc ||
^|| = |v |
ça suffit pour calculer la norme de la force
D'accord...! Tout simplement alors. Je pensais qu'il fallait faire intervenir les vecteurs unitaires du repère mobile.
Merci beaucoup!
ton calcul complet est juste, et tu retrouves le résultat évidemment, mais il est inutile donc tu perds tu temps
Annuler
connectez vous