Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

TP optique : PRISME

Posté par
kamikaz 29-12-21 à 10:42

Bonjour et bonne fêtes à tous.

Je dois faire un compte rendu du TP sur les prismes, mais j'ai un soucis avec certaines valeurs.

BUT DU TP.

- Détermination de l'indice de réfraction n d'un prisme en verre.

- Détermination des coefficients A et B de la formule de Cauchy n =\text{A}+\text{B}\left(\dfrac{1}{\lambda ²}\right).

- Après avoir tracé les courbes n = f\left(\dfrac{1}{\lambda ²}\right), déterminer les coefficients A et B. Calculer
les pouvoirs dispersifs du verre

Est ce que la variation de Dm = 286 0,2 que je donne est juste ?



Les résultats des différentes mesures sont consignés dans le tableau suivant :

RaiesDoublet jauneDoublet jauneDoublet VertDoublet bleuDoublet indigoDoublet violet
(nm)579,1577546491,3435,8404,7
355,06°355,016°354,08°353°351,31°350,33°
'67,16°67,16°67,16°67,16°67,16°67,16°
Dm = |'-|287,9287,86286,92285,84284,15283,17
=(Dm+A)/2203,925203,905203,435202,895202,050201,560
sin-0,4055-0,4052-0,397-0,389-0,375-0,367
n-0,4687-0,4683-0,4596-0,4496-0,4339-0,4247
n
1/² (m²)2,982.10123,004.10123,354.10124,143.10125,265.10126,105.1012


\blue{\text{A} = \dfrac{|\alpha_1 - \alpha_2 |}{2} = \dfrac{|118,16°-358,06°|}{2} = 119,95° ~ \text{et} \sin\left(\dfrac{A}{2} \right) = 0,8658 \\ \blue{ \text{Pour le calcul de  } \Delta n,~ \text{on utilise l'incertitude sur  } \ln(n).\text{ En effet, on a :  } \ln(n) = \dfrac{\Delta n}{n}~ \text{donc  } \Delta n = n \ln(n)~~;~~ \ln(n) = \ln(\sin(\phi))-\ln \left(\sin\left(\dfrac{A}{2}\right)\right)}} \\\\\\ \blue{n =\dfrac{\sin\left(\dfrac{A+D_m}{2}\right)}{\sin\left(\dfrac{A}{2} \right)}}~\text{avec A = 120° et }~ \text{D}_m = (286 \pm 0,2)° \\\\\\ \blue{\dfrac{dn}{n}=\dfrac{d\left(\sin\left(\dfrac{A+D_m}{2}\right)\right)}{\sin\left(\dfrac{A+D_m}{2}\right)}-\dfrac{d\left(\sin\left(\dfrac{A}{2}\right)\right)}{\sin\left(\dfrac{A}{2}\right)} = \left[ \dfrac{1}{\tan \left(\dfrac{A+D_m}{2}\right)} -\dfrac{1}{\tan \left(\dfrac{A}{2}\right)}\right] \dfrac{dA}{2}+\left[\dfrac{1}{\tan \left(\dfrac{A+D_m}{2}\right)}\right] \dfrac{dD_m}{2}} \\\\\\ \blue{\dfrac{\Delta n}{n} = \left[\dfrac{1}{\tan \left(\dfrac{A+D_m}{2}\right)}\right] \dfrac{\Delta D_m}{2}~~ \text{puisque   }\Delta A = 0}~\text{et  }\Delta D_m ~ \text{est en radian !}

Du coup je n'arrive pas à remplir la ligne pour \Delta n car j'ai que des valeurs négatives pour n.

Posté par
vanoisere : TP optique : PRISME 29-12-21 à 12:41

Bonjour
Tes valeurs de la déviation minimale sont totalement irréalistes. Aide-toi d'un schéma représentant les rayons déviés dans les deux cas. Tu devrais aboutir à des valeurs de Dm voisines de70°. Même chose pour l'angle au sommet du prisme. Tu as manipulé ce prisme : tu as bien dû te rendre compte que son angle au sommet est très inférieur à 120°. Classiquement : A est très proche de 60°

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 12:52

En fait c'est le cas sur les autres paillasses de la salle de TP.

Mais dans notre cas on avait bien ces valeurs..

Posté par
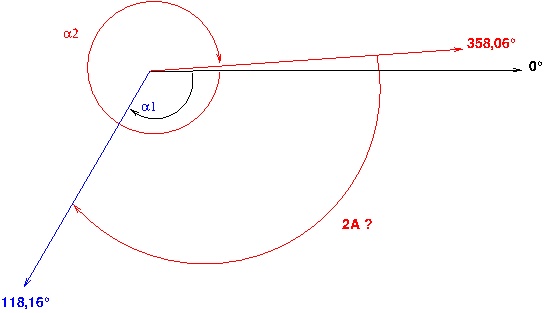
vanoisere : TP optique : PRISME 29-12-21 à 14:05

Tes mesures sont à mon avis tout à fait correctes. C'est leur exploitation qui est fausse et irréaliste. Tu ne gères pas correctement la discontinuité de 360° dans les graduations du cadran du goniomètre : le passage de 359,99° à 0,00°. Aides toi d'un schéma pour bien comprendre. Tu peux aussi raisonner en mesures algébriques et supprimer la discontinuité d'affichage en remarquant que, pour un affichage supérieure à 180°, il est commode  de soustraire 360° à la mesure sans modifier son sens physique.
Tes mesures de 1 et 2 conduisent à : A=60,00° : c'est la valeur constructeur !
Pour la première raie du doublet jaune, j'obtiens :
Dm=72,10° ; valeur réaliste...

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 14:25

Donc \alpha_1 = 118,16° et \alpha_2 = 358,06° > 180° \Rightarrow \alpha_2 = 360°-358,06° = 1,94°

Je trouve A = 58,11°

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 15:16

Comment faire pour la courbe n = f\left(\dfrac{1}{\lambda ²}\right) ?

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 16:33

D_m = 48 \pm 0,2 non ?

Posté par
vanoisere : TP optique : PRISME 29-12-21 à 17:10

Tu n'as pas compris mes messages  précédents. Je fais un schéma illustrant la détermination de l'angle A. Je te laisse faire pour Dm...
Pour le tracé, tu portes dans un repère les points de coordonnées :
x=1/2
y=n
Si la loi est vérifiée, tu devrais obtenir des points sensiblement alignées le long d'une droite moyenne d'équation :
y=A+B.x
Les tableurs et la plupart des logiciels scientifiques font cela très bien...

TP optique : PRISME

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 18:31

Mais A = 58,11° non ?

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 18:34

Citation :
Pour la première raie du doublet jaune, j'obtiens :
Dm=72,10° ; valeur réaliste...


Moi je trouve Dm = 62,22°

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 18:37

Ah oui je vois.

Posté par
vanoisere : TP optique : PRISME 29-12-21 à 18:47

Citation :
Ah oui je vois.

J'espère que cela va te permettre de rectifier les valeurs que tu indiques dans tes deux précédents messages. Elles sont incohérentes avec tes mesures dans les deux cas...

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 19:27

Oui  je trouve la même chose que toi pour le la première raie du doublet jaune et je crois que c'est bon pour le reste.

\alpha_2 = -1,94° ; A = 60,05°

Posté par
vanoisere : TP optique : PRISME 29-12-21 à 19:35

Afin de t'auto-corriger, voici le positionnement des points expérimentaux (petites croix rouges) , le tracé de la droite moyenne et son équation.

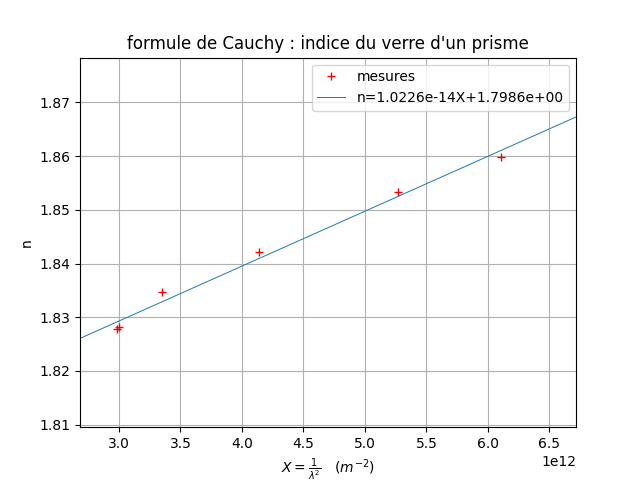
TP optique : PRISME

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 20:13

OK, çà passe

Posté par
kamikazre : TP optique : PRISME 29-12-21 à 21:03

\text{n = A +B}\left(\dfrac{1}{\lambda ²}\right)

1,826 = \text{A+B}*2,98.10^{12}~(1)

1,858 = \text{A+B}*6,105.10^{12}~(2)

De (1) et (2) ; on a le système suivant : \begin{cases} 1,826 = \text{A+B}*2,98.10^{12} \\ 1,858 = \text{A+B}*6,105.10^{12} \end{cases} \Rightarrow \begin{cases} \text{A} = 1,795 \\ B = 1,024.10^{-14} \end{cases}

On vérifie bien que \text{n = A +B}\left(\dfrac{1}{\lambda ²}\right).

Merci beaucoup.

Posté par
vanoisere : TP optique : PRISME 30-12-21 à 14:42

Tes valeurs sont très proches de celles fournies par le programme de tracé de la droite moyenne.Juste une remarque : B se mesure en m-2 puisque tu as exprimé en mètre.
Le faible écart s'explique sans doute par le fait que tu as choisi pour obtenir l'équation deux points expérimentaux qui sont très proches de la droite moyenne sans appartenir à celle-ci.

Posté par
kamikazre : TP optique : PRISME 31-12-21 à 13:00

OK


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !