Inscription / Connexion Nouveau Sujet
TP mécanique
Bonjour,
Il y'a un TP de résonnance mécanique d'un oscillateur amorti qui me perturbe. On a deux pendule, l'un appelé résonnateur, c'est un pendule en fer je pense, sur lequel est fixé une masse au milieu (et qu'on peut déplacer) et sur lequel est fixé une plaque métallique (pour le frottement fluide). L'autre pendule appelé excitateur, c'est une tige en métal sur laquelle glisse une grosse masse cylindrique (tige et masse forme un pivot glissant). Il y'a un support gradué en cm sur lequel est fixé l'axe de rotation des deux pendules, chacun se trouvant dans une partie du support. De plus, le résonnateur est lié au support par un ressort.
On nous demande de calculer la période propre de chacun des deux pendules d'abord.
Normalement, la période propre c'est en l'absence d'excitation et de frottements et en travaillant avec les faibles angles. Car, en présence d'excitation, on serait entrain de mesurer une période "induite". En présence de frottements, on mesurerait des pseudo-périodes. Et si on travaille pas en faibles angles alors la période qu'on mesure dépend des conditions initiales.
C'est à partir de ce raisonnement que je fixe l'excitateur (par ma main) et j'enlève la plaque qui impose le frottement et j'essaye de calculer la période propre du résonnateur, mais le professeur m'a demandé de la remettre et de ne rien enlevé. Quand j'essaye de travailler en faibles angles, je trouve des résultats très dispersés. Mais quand j'augmente bien l'angle initial (dans les 30°) alors je trouve des résultats très peu dispersés (10-3) autour d'une valeur moyenne de 1.3s
Je comprends qu'en augmentant l'angle initial, on donne plus d'énergie cinétique initialement, ce qui permet de "triompher" du frottement au début. Et comme la durée d'acquisition n'est pas très longue alors on ne se rend pas compte du frottement.
Je me demande si mon raisonnement est correct, car sinon le TP serait hypocrite en fermant l'oeil sur tous ces problèmes.
J'espère que vous pourrez m'affirmer si ce que je dit est correct ou m'expliquer les fautes de mon raisonnement.
Merci d'avance,
Bonjour
Comme déjà souvent dit : conseiller sur un TP sans connaître les objectifs de celui-ci et surtout sans connaître le matériel à disposition....
Ayant mesuré la période T pour une amplitude , tu peux revenir à la période propre par la relation que tu as sans doute démontrée en cours et que j'ai eu l'occasion de démontrer ici (pages 11 et suivantes)
![]() ou par la formule approchée de Borda :
ou par la formule approchée de Borda :
Bonjour,
Veuillez excuser mes piètres compétences en dessin, j'ai essayé de faire un schéma qui représente le matériel.
L'objectif du TP est de tracer la courbe de résonnance (  positions maximale atteinte par le résonnateur en fonction de la fréquence de l'excitateur ).
positions maximale atteinte par le résonnateur en fonction de la fréquence de l'excitateur ).
Je pense que les formules auxquelles vous faites allusion (celle dans le PDF , qui est très enrichissant au passage, et celle de Borda) ne fonctionnent que si l'oscillateur n'est pas amorti je suppose.
Mais de toute façon, au TP on m'avait dit de juste calculer la période des oscillations, mais la question portait sur la période propre.
Merci d'avance,
Si les frottements sont faibles, en oscillations libres, la mesure de T à amplitude moyenne permet d'obtenir la période propre To par la formule de Borda ; la période propre est la période des oscillations avec amplitude très faible en absence de frottement et d'excitation.. Tu parles de résonance d'amplitude. La théorie au programme suppose un excitateur de période d'excitation fixe. Avec ce genre de matériel, si j'imagine correctement bien sûr, il est très difficile d'obtenir ce résultat ; même en choisissant deux pendules de masses très différentes, on obtient presque toujours un phénomène de battement. Le pendule de Pohl permet une étude précise du phénomène mais le matériel est assez coûteux...
Je m'excuse. Encore une maladresse de ma part. Je télécharge l'image et j'oublie de l'attacher.
Je ne mesurais alors que T, je pense que le professeur négligeait l'amplitude du mouvement, mais c'était quand même une amplitude de 30°...
Quand j'ai essayé d'enlever la plaque pour réduire le frottement on m'a demandé de la garder.
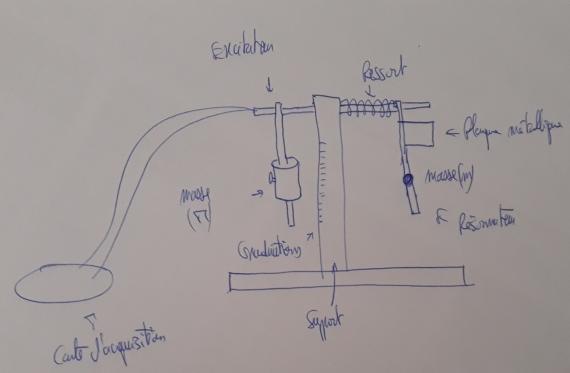
Merci pour le schéma. Lorsque les deux pendules oscillent, l'amplitude de l'excitateur reste-t-elle, après bien sûr un régime transitoire, indépendante du temps ? Si oui : tout va bien, tu vas pouvoir interpréter les mesures en considérant que ton résonateur est un oscillateur soumis à une excitation périodique. L'étude est analogue à celle de la résonance de charge dans un circuit RLC série en régime sinusoïdal.
Si non : problème : il faut considérer le système comme un système constitué de deux oscillateurs couplés ; tu obtiens des battements.
Bonjour,
Merci pour votre réponse. Oui, l'amplitude de l'excitateur reste indépendante du temps. Je n'ai pas de problème avec l'étude de la résonnance, mon souci reste la détermination de la période propre du résonnateur car je pense que ce qu'on a fait ne concordait en rien avec la réalité (je n'ai mesuré que la période du résonnateur en l'écartant de 30° de sa position d'équilibre). Je ne pense pas que les frottements soient très faibles pour les négliger et utiliser la formule de Borda.
Une autre question, j'ai essayé ce matin d'établir l'équation différentielle du mouvement du résonnateur et j'ai bloqué au niveau du moment de la force de frottement .Je pense qu'avec des calculs très lourds et en passant par les coordonnées cartésiennes (j'ai du mal à écrire
rigoureusement puisque cela va dépendre de
à laquelle on rajouterait une constante pour décrire toute la plaque) on pourrait simplifier un peu l'intégrale, mais je n'ai pas eu le courage de m'aventurer dans cette voie. J'aimerais vous demander s'il y'a une méthode pour exprimer ce moment.
Merci d'avance,
Pour la période propre : reprends ton cours sur la pseudo période du mouvement pseudo périodique ; pour des frottements faibles, l'écart entre pseudo période et période propre est très faible. Tu peux donc négliger l'existence des frottements pour déterminer To. En revanche, l'influence de l'amplitude n'est pas négligeable, d'où l'intérêt de la formule de Borda.
Il est extrêmement délicat de modéliser correctement l'action du fluide sur la pale. La méca des fluides : c'est loin d'être simple ! Dans le cadre de ton programme, on se contente habituellement de considérer que le moment de cette action par rapport à l'axe de rotation est proportionnel à la vitesse angulaire :
Merci pour votre réponse.
Il fallait donc impérativement utiliser la formule de Borda.
Jusqu'à quel ordre de grandeur on peut encore utiliser la formule de Borda s'il vous plaît ? (Par exemple pour l'approxmation des faibles angles c'est jusqu'à 15°)
Tout dépend de la précision attendue ! Sur le document que je t'ai indiqué, j'ai représenté page 12 l'écart de période entre calcul exact et formule approchée de Borda en fonction de l'amplitude angulaire. Sur un document destiné à des physiciens et non à des passionnés d'horlogerie, j'aurais porté en ordonnées l'écart relatif et non le retard hebdomadaire de l'horloge. Pour ne pas refaire le tracé, il te suffit de savoir qu'un écart relatif de 0,1% correspond à un retard hebdomadaire d'environ 300s, ce qui correspond à une amplitude angulaire d'environ 40°. Pas de problème ici pour utiliser la formule de Borda.


