Inscription / Connexion Nouveau Sujet
TP - Disque roulant sur rail inclinés
Bonjour,
Ayant une préparation de TP à faire en Mécanique du Solide, je bloque sur une question. Voici l'énoncé :
I/ Moment d'inertie
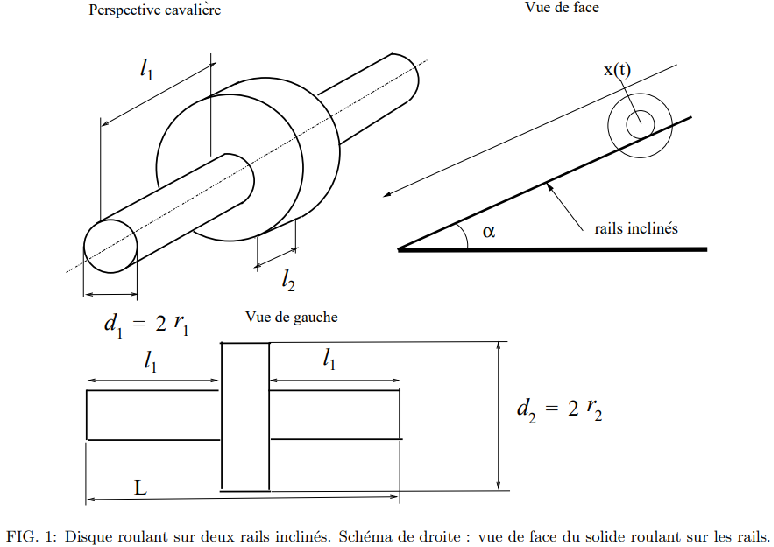
Calculer le moment d'inertie I autour de son axe, pour le solide dessiné sur la figure 1, en fonction des deux rayons r1 et r2. r1 est le plus petit rayon et r2 le plus grand, et des deux longueurs l1 et l2. La longueur l2 correspond à l'épaisseur du disque interne. La longueur totale du solide est L = l2 + 2l1. Vérifier que l'on retrouve le moment d'inertie d'un cylindre simple dans les deux cas r1 = r2 et l1 = 0.
-> J'ai fais cette question et j'ai trouvé
II/ Mouvement sur des rails inclinés
a) Un tel disque (avec moment d'inertie I par rapport à son axe de symétrie) roule sur deux rails inclinés d'un angle α par rapport à l'horizontale. On prend comme instant initial t0, la vitesse est nulle pour t = t0. Pour calculer la position de l'axe du disque x(t) en fonction du temps, on exprimera l'accélération aeff = d2x/dt² sous la forme
aeff = où m est la masse totale du disque roulant et F une fonction à préciser. Le rapport I/(mr1²) est sans dimension. g est l'accélération de la pesanteur. On prendra g = 9, 81m.s^−2. Que se passe-t-il dans le cas r2/r1 très grand ?
b) On mesure les temps de passage ti à plusieurs positions xi. Etablir une formule pour déterminer aeff à partir des ti et des xi sans avoir à faire intervenir t0. En effet, t0 est expérimentalement assez mal connu par les mesures avec les capteurs optiques.
c) Même question qu'en II.a, mais pour une boule et un cylindre roulant sur une planche. On peut utiliser la formule qui donne le moment d'inertie d'une sphère de masse M par rapport à un axe contenant son centre, I =2*M*r2/5, sans chercher à la démontrer.
C'est pour la partie 2 que je bloque. (question a,b et c)
-> Par analyse dimensionnelle, F doit être sans dimension mais je n'arrive pas à trouver son expression. Aussi, à quoi fait fait référence aeff ?
Bonjour
En négligeant les frottements, tu peux considérer que l'énergie mécanique de ton solide se conserve.
L'énergie mécanique peut s'écrire, à une constante près :
Le théorème de Koenig n° 3 permet d'écrire l'énergie cinétique sous la forme :
en supposant le roulement sans glissement.
Ecrire ensuite que la dérivée par rapport au temps de l'énergie mécanique est nulle à chaque instant permet d'obtenir l'accélération par rapport au repère terrestre supposé ici galiléen.
Réflexion faite, il serait plus simple de poser :
aeff me semble désigner tout simplement l'accélération du centre d'inertie du solide dans le repère terrestre.
F désigne une fonction de la grandeur . Effectivement,
est une grandeur sans dimension (grandeur de dimension 1 comme on dit encore).
Nos deux messages de 16h21 se sont croisés. D'accord avec ton expression de l'accélération du centre d'inertie G du solide. Je ne vois pas trop l'intérêt de l'indice "eff"...
Je pense qu'il faut comprendre , grandeur sans dimension caractérisant les importances relatives de l'énergie cinétique de rotation et de l'énergie cinétique de translation ; la formule montre clairement que, plus le moment d'inertie est grand à m et r1 donnés, plus l'accélération est faible.
J'avais trouvé cela aussi.
Pour la question b, on sait que a = d²x/dt² = dv/dt et que v = x/t mais je ne vois pas comment faire entrer les xi et ti. A première vu, j'aurais dit que
vi = xi/ti
Il existe une méthode simple et rapide pour régler le problème lié à to à condition de disposer d'un ordinateur avec un tableur (Excel, LibreOffice...) ou d'une calculatrice moderne.
Imagine que le démarrage en x=0 avec une vitesse nulle n'ait pas lieu à la date zéro mais à une date to . On peut écrire, puisque le mouvement est uniformément accéléré :
On place les points de coordonnées (ti,xi) dans un repère et on demande au tableur de tracer la courbe de tendance correspondant à la fonction polynôme de degré 2. Le tableur donne alors l'équation de la parabole passant au plus près des points expérimentaux sous la forme :
f(X)=A.X2+B.X+C
Par identification : ce qui donne une bonne mesure de a, d'autant meilleure que la valeur absolue du coefficient de corrélation est proche de 1.
On peut éventuellement faire cela "à la main" :
Pour le premier point fiable de mesure :
Pour les autres points avec i=2,3,... :
soustraction « membre à membre » :
On remplit un tableau de mesures....
x_{i}=\frac{1}{2}a.\left(t_{i}-t_{0}\right)^{2}
Je ne comprends pas comment vous avez trouvez ceci. Vous êtes partit de a = d²x/dt² ?
Oui ! Dans la mesure où les frottements sont négligeables, l'accélération est une constante :
intégration par rapport au temps :
si t=0 correspond à un départ à vitesse initiale nulle.
Intégration par rapport au temps :
avec xo=0 si l'origine des abscisses est choisie comme position initiale.
Si la situation (x=0, v=0) ne correspond pas exactement à t=0 mais à t=to, il y a lieu dans les équations précédentes de remplacer t par la durée effective du mouvement (t-to).


