Bonjour
Tu ne pourrais pas poster un scan du schéma et un résumé de l'énoncé ? Sinon : difficile de t'aider...

Bonjour, Oui bien sur j'ai (comme bien souvent) oublié d'attacher l'image

Tout va bien pour l'instant. Pas de soucis pour ton vecteur rotation instantané du disque.

super merci !

En calculer les matrices ,
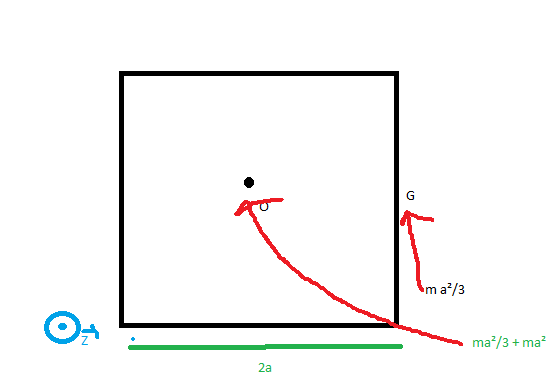
- Pour le cadre, (coté 2a masse m)  seul le calcul de "C" est utile (le vecteur rotation du cadre est suivant z₀ uniquement)
Je trouve 4* (m a²/3 + ma²) (en faisant pour une barre en G puis en transposant en O via Hugens et en multipliant le tout par 4)

-Pour le disque (rayon r, masse M) je trouve

Pour pouvoir multiplier cette dernière matrice par , je dois projette ce vecteur u suivant x,y et z, c'est ça ? Ou on peut multiplier directement sans que cela pose soucis ?

Merci encore et bonne soirée  

Après réflexion la matrice d'inertie du disque est exprimée dans sa base, c'est à dire (u, v, z) (et pas u, v₀, z₀ comme je l'avais écrit avant)

Le problème serait donc la multiplication de cette matrice avec le du disque (pour le torseur cinétique) ?

Merci d'avance

Bonsoir
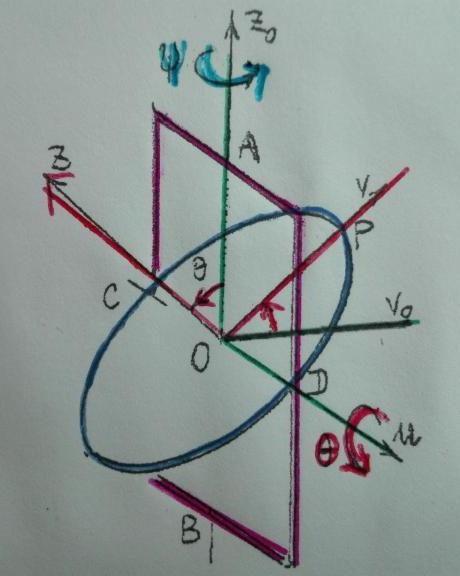
Je ne comprends pas bien les différents repères utilisés.  Il me semble que par rapport à un repère terrestre fixe Ro, le cadre peut tourner autour de l'axe (Oz_o) fixe. En même temps le disque peut tourner autour de son diamètre CD. Dans ce cas, le centre de gravité de chaque solide est fixe et confondu avec le point O ???
Comment sont définis exactement les deux repères liés à chacun des deux solides ?
Peux-tu scanner et poster un autre schéma plus complet ?

Bonsoir et merci pour votre réponse,

•Il y a un premier référentiel (terrestre) fixe (x_0, y₀, z₀) . (pas représnté sur la schéma)
•Un deuxième référentiel (u,v₀,z₀) lié au cadre est créé, après sa rotation de autour de
• Un troisième référentiel (u,v,z) lié au disque esr créé après sa rotation de suivant

Je peu essayer de faire moi même un schéma et le poster si vous souhaitez


Merci d'avance pour votre aide

PS : Après correction, j'ai trouvé, pour le C de la matrice du cadre en O,
C = C_{2barres horizontales} + C_{2barres verticales} = 2 * [(ma²/3) + a²m] + 2 [ 0 + a²m]

Et j'ai effectivement considéré que le centre de gravité du cadre et du disque sont confondus en O et fxes (d'où la vitesse V_O  nulle dans les torseurs )

Merci pour les précisions. Je pense avoir compris les notations maintenant.
Concernant C pour le cadre. Je ne vois pas vraiment l'intérêt de faire intervenir le théorème de Huygens.
Pour les côtés verticaux : la totalité de la masse se trouve à la distance a de l'axe. La définition du moment d'inertie par rapport à un axe conduit sans calcul à m.a² pour chacun des deux côtés.
Pour les côtés horizontaux : l'axe Oz_o passe par le centre de gravité de chaque côté. Que viendrait donc faire ici le théorème de Huygens ? Il s'agit du calcul ultra classique du moment d'inertie d'une tige homogène par rapport à un axe perpendiculaire à cette tige passant par son milieu. Cela donne m.a²/3 par tige. Sauf erreur :


Même si ce n'est pas directement utile pour la suite : A=C ; B=A+C.
OK pour la matrice d'inertie du disque homogène.

Merci beaucoup pour votre aide

- Pour la matrice du cadre, pour les cotés horizontaux, je pensais calculer le moment d'inertie de la barre en son centre de masse (ce qui donne a²/3 )  et transposer au point O via Huygens (et la distance entre Gz et Oz vaut 0, ) donc on retrouve bien votre résultat
(notre cours ne traite que des moments d'inertie par rapport à un point car apparemment c'est plus simple que  par rapport à un axe)
J'avais commis de nombreuses erreurs (sur les bornes d'intégration j'avais 0 et 2a au lieu de -a et a) mais j'ai bien compris

- Cependant, pour le torseur cinématique du disque, comment multiplier la matrice obtenue par ?

La matrice de ce disque étant valable pour les axes (u,v,z) et pas z₀ ...
Projette z₀ sur z et v ?


Merci encore

Belle soirée !

L'énoncé nous dit d'évaluer, en fonction des données (masses et dimensions des solides) et des paramètres de leur mouvements (angles et )
1) Le torseur cinématique de chaque solide
2) Le torseur cinétique de chaque solide
3) Le torseur dynamique de chaque solide
4) L'énergie cinétique de chaque solide
Nous n'avons aucune indication concernant la base d'expression de tous ces torseurs ...




Cela donne donc, pour le moment cinétique du disque


En posant (sous réserve de vecteur normés)


C'est bien ca ?


Cela donne un vecteur exprimé dans la base mobile (u,v,z), et si on doit exprimer cela dans R₀ = (x₀ y₀, et z₀) , et rédériver pour avoir le moment dynamique, les calculs seront horribles, non ?

Merci pour votre aide

Bonne journée

Pour le calcul de l'EC, qui correspond à la moitié du produit du torseur cinématique et du torseur cinétique, cela pose soucis de multiplier (dans le cas di disque)
- Le vecteur rotation instantané (exprimé en base (x₀,y₀,z₀)
avec
- Le vecteur moment cinétique (exprimé en base (u,v,z) )
?

Je trouve bizarre que nous n'ayons jamais eu besoin en cours de tout ramener à la base R₀ et qu'il y ai besoin de le faire pour ce DM


Merci encore

Bonne journée

C'est la même chose pour l'énergie cinétique. Il faut utiliser les vecteurs rotation instantanés traduisant les mouvement par rapport à Ro mais ces vecteurs doivent être exprimés dans la même base que la matrice d'inertie.

Donc pour le vecteur rotation du disque je trouve

Cela est-il correct ? (j'ai un doute sur la projection)

Pour la matrice exprimée en base (u,v,z) je pense la multiplier avec le vecteur rotation, en base (u,v,z) puis mettre le résultat obtenu en base R₀ , cela est il exact ?


Merci encore pour votre aide précieuse

Bonne soirée

On ne s'est pas bien compris.
Pour le disque, puisque la matrice d'inertie est exprimer dans le repère (u,v0,z0), il faut commencer par expliciter le vecteur rotation instantanée du cadre dans ce même repère. Pas de problème bien sûr.
Pour le disque, c'est le même principe : puisque la matrice d'inertie est explicitée dans le repère (u,v,z), il faut aussi expliciter le vecteur rotation instantané du disque dans ce même repère.

Bonjour,

Cela donne donc, sij'ai bien compris,  en base (u,v,z) ,

Pour la calcul de l'EC, où on fait le produit scalaire du vecteur rotation et du moment cinétique *0.5 (car ici V_O = 0), on peut rester en base (u,v,z) sans que cela pose soucis (et avoir à juste exprimer z₀ en fonction de v et z ) ?


Merci encore pour votre aide

Bon dimanche !

avec une erreur d'inversement de et dans le vecteur

Merci beaucoup Vanoise pour tous ces éclaircissements

Nous avons réussi (en faisant bien attention à ne pas "mélanger" les bases) à répondre aux questions du dm

L'expression du moment dynamique du disque est assez horrible (nous avons utilisé la formule de Bour) : cela mèneà la dérivée classique dans R2 +   un produit vectoriel du style  (..u + ..v + ..z) ^(...y + ...v + ...z) mais je ne vois pas d'autre moyen d'y arriver


Merci encore

bonne soirée