Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... IutForum Supérieur (IUT) PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau iut
Partager :

Torseurs

Posté par
aua 23-02-25 à 21:34

Bonjour, j'espère que vous allez tous très bien
J'ai dû mal à comprendre quand effectuer des changements de repère avec les torseurs, ou du moins quand cela est il permis. Merci d'avance de votre aide !
Voici un exercice pour illustrer ce que je veux dire

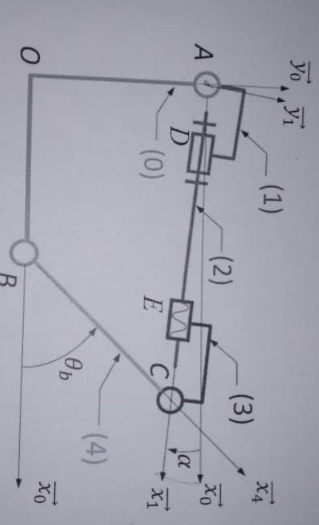
Torseurs
\vec{OA}=a.\vec{y_{0}} , \vec{OB}=b.\vec{x_{0}} , \vec{BC}=c.\vec{x_{4}}
1. Tracer le graphe des liaisons
2. Ecrire le torseur d'actions mécaniques de chaque liaisons
3. Exprime en O, la somme des torseurs des liaisons en A, B et C

Posté par
auare : Torseurs 23-02-25 à 21:53

1-Torseurs

2-
T_{(S0-S1)A}=\begin{Bmatrix} X_{10} & L_{10} \\ Y_{10}& M_{10}\\ Z_{10}& 0 \end{Bmatrix}_{A}
T_{(S1-S2)D}=\begin{Bmatrix} X_{12} & 0 \\ Y_{12}& M_{12}\\ Z_{12}& N_{12} \end{Bmatrix}_{D}
T_{(S2-S3)E}=\begin{Bmatrix} X_{23} & \frac{\pm P}{2\pi }X_{23} \\ Y_{23}& M_{23}\\ Z_{23}& N_{23} \end{Bmatrix}_{E}
T_{(S3-S4)C}=\begin{Bmatrix} X_{34} & L_{34} \\ Y_{34}& M_{34}\\ Z_{34}& 0 \end{Bmatrix}_{C}
T_{(S4-S0)B}=\begin{Bmatrix} X_{40} & L_{40} \\ Y_{40}& M_{40}\\ Z_{40}& 0 \end{Bmatrix}_{B}

Posté par
auare : Torseurs 23-02-25 à 21:56

3- J'aimerais savoir quand on définit un torseur,, ce dernier a t il les mêmes coordonnées dans les bases des deux solides. Dans le cas de T10, par exemple, le torseur est il le même qu'on soit dans R1 ou R0 ?

Posté par
gts2re : Torseurs 24-02-25 à 05:51

Bonjour,

Un torseur, c'est l'assemblage de deux vecteurs.
Or vous savez que les composantes d'un vecteur dépendent de la base de projection. Pour un torseur c'est donc la même chose.  
Donc il y a bien un seul T10 mais de projections différentes dans R1 et R0.

Posté par
gts2re : Torseurs 24-02-25 à 06:20

Bonjour,

Sinon pour la première question, il est toujours permis de changer de repère. Cela est utile pour exprimer par exemple le torseur agissant sur 1 : T1=T01-T12 ; si T01 est exprimé dans R0 et T12 dans R1, il faut bien effectuer un changement de base. Ne pas oublier que le point où est exprimé T01 (A) est différent de celui de T12 (D).

Posté par
auare : Torseurs 24-02-25 à 09:34

gts2 @ 24-02-2025 à 06:20

T1=T01-T12

J'ai pas très bien capté cette relation. Comment on l'obtient ?
Concernant la base dans laquelle un torseur est défini, comment l'a choisit on ? C'est arbitraire. Quand on écrit TS[sub]1->S2[/sub] signifie que les coordonnées du vecteur sont dans la base B1 ou B2?
Exemple pour les torseurs cinématiques on sait que:
\left\{\vartheta _{1/0} \right\} est défini dans la Base 0 cela vient tout simplement de l'écriture même du torseur cinématique
Quand est il du torseur statique ?

Posté par
gts2re : Torseurs 24-02-25 à 10:27

Citation :
T1=T01-T12 .  J'ai pas très bien capté cette relation. Comment on l'obtient ?

Le torseur total est la somme des torseurs T(1)=T(0/1)+T(2/1) et troisième loi de Newton T(2/1)=-T(1/2).

La base est en général imposée, sinon on la choisit la plus simple possible selon les liaisons, par exemple pivot : axe du cylindre. C'est la liaison qui "impose" la base donc T12 ou T21, ce sera la même base.

Dans votre cas, les trois liaisons pivot (01, 04, 43) ont le même z, mais on peut prendre xy comme on veut,  donc prendre x1 (puisque axe des liaison 12 et 23). Donc on peut prendre pour base pour toutes les liaisons R1.  

\theta_{10} est l'angle entre x0 et x1, je suppose, c'est le même angle quelque soit la base. Que vouliez-dire ?

Posté par
auare : Torseurs 24-02-25 à 17:57

D'accord je vois
3-Je vais traiter le cas du point C
\vec{M_{O}} = \vec{M_{C}} + \vec{OC}\wedge \vec{R}
Tout en sachant que les coordonnées du torseurs sont dans la base R1
\vec{M_{O}} =\vec{M_{C}}+(\vec{OB}+\vec{BC})\wedge (X_{34}\vec{x_{1}}+Y_{34}\vec{y_{1}}+Z_{34}\vec{z_{1}})
\Rightarrow \vec{M_{O}} =\vec{M_{C}}+(b\vec{x_{0}}+c\vec{x_{4}})\wedge (X_{34}\vec{x_{1}}+Y_{34}\vec{y_{1}}+Z_{34}\vec{z_{1}})
\Rightarrow \vec{M_{O}} =\vec{M_{C}}+(b\vec{x_{0}}+c. cos \theta \vec{x_{0}} +c.sin\theta \vec{y_{0}} )\wedge (X_{34}\vec{x_{1}}+Y_{34}\vec{y_{1}}+Z_{34}\vec{z_{1}})
\Rightarrow \vec{M_{O}} =\vec{M_{C}}+(-X_{34}.sin\alpha+ Y_{34}.cos\alpha )(b+c. cos \theta )\vec{z_{1}} -Z_{34}. (b+c. cos \theta )\vec{y_{0}}-c.sin\theta .X_{34}sin\alpha \vec{z_{1}}-c.sin\theta .Y_{34}.sin\alpha \vec{z_{1}} +c.sin\theta .Z_{34}\vec{x_{0}}



C'est bien cela ? Après je vais amener xo et yo dans la base R1 est ce sera bon?

Posté par
auare : Torseurs 24-02-25 à 17:57

Merci d'avance, le calcul est assez laborieux...

Posté par
gts2re : Torseurs 24-02-25 à 19:15

Question préliminaire : y-a-t-il des questions mécaniques ensuite (torseur agissant sur un solide) ? Parce que le choix suggéré de R1 venait de la simplification de la somme des actions sur D et sur E. Si vous ne vous intéressez qu'à A, C et B, ma suggestion ne tient pas : R0 est plus pratique pour la question 3. Par contre R0 n'est pas simple pour T12 et T23.

Vos calculs ont l'air corrects.
Mais si l'exo s'arrête là, il vaut mieux tout faire dans R0 (désolé si c'est le cas...)

Posté par
auare : Torseurs 25-02-25 à 18:25

D'accord, merci beaucoup
Ps: oui, l'exo s'arrête là


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !