Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Tige homogène

Posté par
fidele11 26-05-21 à 23:17

Bonsoir,
Besoin d'un coup de main pour cet exercice:

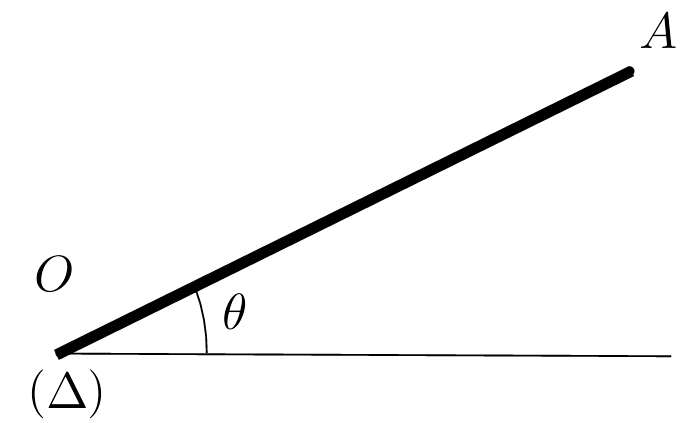
Une tige OA homogène de masse m de forme régulière de longueur L mobile autour d'un axe horizontal (Delta) passant par O fait un angle ∅ avec l'horizontale. À son extrémité A est fixé un godet de masse négligeable. Dans ce godet on dépose une bille ponctuelle.
1. Quel est le moment d'inertie de la tige par rapport à (Delta) ?
2. La tige est lâchée à partir de l'inclinaison ∅0 sans vitesse initiale.
2.1. En appliquant le théorème de l'énergie cinétique, trouver l'expression de la vitesse angulaire ∅' lorsque l'inclinaison vaut ∅.
2.2 Exprimer l'accélération normale du point A.
3. Par dérivation du carré de la vitesse angulaire trouver l'accélération angulaire ∅" de la tige puis l'accélération normale du point A.  
4. Trouver la composante verticale de l'accélération az du point A. Quelle est la valeur initiale de az (lorsque ∅=∅0).
5. En déduire à quelle condition la bille quitte le godet dès le début du mouvement de la tige. (La bille suivant alors une trajectoire verticale). On prendra g=10m/s².


1)
D'après le théorème de Huygens, le moment d'inertie de la tige est:
J=(1/12)mL² + m(L/2)²=(⅓)mL².

2.1) Théorème de l'énergie cinétique :
Ec_{f}-Ec_{i}=W(\vec{F}_{ext})

<=> ½J∅'²-0=W(P)
Mais il me semble que que W(P)=0 car le poids est perpendiculaire au déplacement ...et le reste devient bizarre

Posté par
fidele11re : Tige homogène 26-05-21 à 23:28

schéma :

Tige homogène

Posté par
vanoisere : Tige homogène 27-05-21 à 15:32

Bonjour
D'accord pour le moment d'inertie puis l'application du théorème de l'énergie cinétique.

Citation :
car le poids est perpendiculaire au déplacement

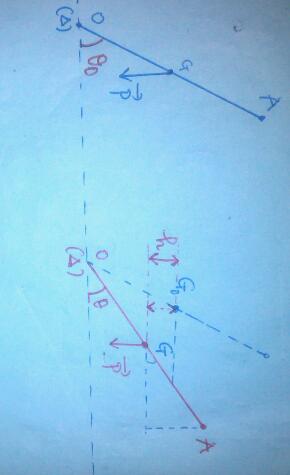
Pas systématiquement au cours de la rotation. Refait une figure en représentant la tige dans la position initiale et dans sa position finale. L'altitude de son centre de gravité aura diminué d'une hauteur h qu'il est facile d'exprimer en fonction de la longueur de la tige et des angles...

Posté par
fidele11re : Tige homogène 27-05-21 à 21:29

2-1) J'ai représenté en (1) la position initiale ∅_0 (que je n'ai pas spécifié ) et en (2) la position de la tige lorsque l'angle entre elle et l'horizontale est ∅.
L'énergie cinétique initiale est nulle et l'énergie cinétique en (2) est ½J∅'².

Le poids étant la seule force qui travaille :
½J∅'²=W(P)=mg*KG
; KG étant la diminution   du centre d'inertie G de la tige.

  Et j'ai trouvé KG=½L(1-cos∅).
Soit W(P)=½mgL(1-cos∅)=½J∅'²
J=⅓mL² Donc j'obtiens après arrangement :
∅'²=(3g/L)(1-cos∅)
Soit ∅'=√(3g(1-cos∅)/L).

2-2) L'accélération normale est a(n)=V²/L avec V=L∅' => a(n)=L∅'².
En remplaçant ∅'² par son expression, => a(n)=3g(1-cos∅).

3) *La dérivée du carré de la vitesse est : ∅"²=(3g/L)sin∅ .Donc l'accélération angulaire est ∅"=√[(3g/L)sin∅].
*Pour l'accélération normale du point A, je n'ai aucune idée ... Est-ce la même accélération demandée en 2.2) (?)

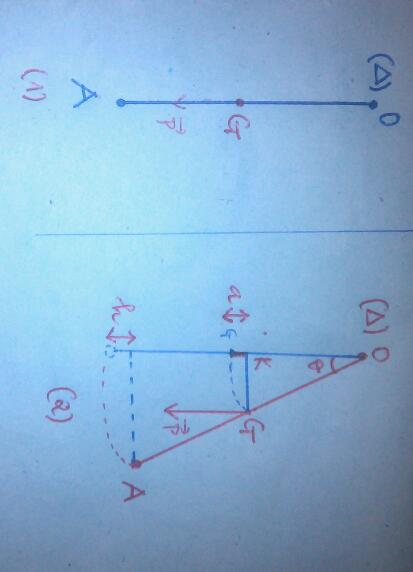
Tige homogène

Posté par
vanoisere : Tige homogène 27-05-21 à 22:53

Selon l'énoncé, l'angle est l'angle entre la tige  et l'horizontale  alors que sur ta figure, il s'agit de l'angle entre la tige et la verticale.
La valeur initiale o n'est pas précisée.  De toutes les façons, l'altitude initiale de G est supérieure à l'altitude de G à la position d'angle et la valeur h qui intervient dans l'expression du travail du poids est la différence d'altitude de G entre la position d'angle o et la position d'angle .

Posté par
fidele11re : Tige homogène 27-05-21 à 23:00

Ok d'accord

Posté par
fidele11re : Tige homogène 28-05-21 à 11:07

Bonjour,
Donc l'expression de la vitesse angulaire s'exprimera en fonction de l'angle ∅_0 et ∅ ? comme la variation de G est h-h_0 ..

Posté par
vanoisere : Tige homogène 28-05-21 à 12:58

Citation :
Donc l'expression de la vitesse angulaire s'exprimera en fonction de l'angle ∅_0 et ∅ ?

Oui. Il te faudrait refaire un schéma montrant la tige dans sa position initiale et la tige dans une position quelconque. Les deux angles devraient apparaître clairement sur ce schéma.

Posté par
fidele11re : Tige homogène 28-05-21 à 21:14

Voici ce que j'ai refait

Tige homogène

Posté par
fidele11re : Tige homogène 28-05-21 à 21:48

Voici ce que je trouve alors pour la vitesse angulaire:
On avait \frac{1}{2}J\theta'^{2}=mgh

Avec h=\frac{Lsin\theta_{0}}{2}-\frac{Lsin\theta}{2}

Ainsi \frac{1}{2}J\theta'^{2}=mg(\frac{Lsin\theta_{0}}{2}-\frac{Lsin\theta}{2})
J=\frac{1}{3}mL^{2}

Donc j'obtiens: \theta'^{2}=\frac{3}{L}(sin\theta_{0}-sin\theta)
Soit \theta'=\sqrt{\frac{3}{L}(sin\theta_{0}-sin\theta)}

Posté par
vanoisere : Tige homogène 28-05-21 à 23:06

Tu as oublier de taper le "g" dans les dernières formules mais le raisonnement est correct. Merci de faire l'effort d'utiliser l'éditeur d'équations. C'est tellement plus lisible !

Posté par
fidele11re : Tige homogène 29-05-21 à 00:38

Ok je devrais avoir,
\theta'^{2}=\frac{3g}{L}(sin\theta_{0}-sin\theta)
Soit \theta'=\sqrt{\frac{3g}{L}(sin\theta_{0}-sin\theta)}

2.2) Accélération normale du point A.
a_n=\frac{V^2}{L} avec V=L\theta' <=> a_n=L\theta'^2=3g(sin\theta_{0}-sin\theta)

3. La Dérivée de la vitesse angulaire est:
\frac{d\theta'^{2}}{d\theta}=\frac{-3g}{L}cos\theta

Posté par
fidele11re : Tige homogène 29-05-21 à 00:43

je ne vois pas comment trouver l'accélération normal du point A à partir de cette dérivée seconde

Posté par
vanoisere : Tige homogène 29-05-21 à 12:37

Tu peux dériver par rapport à t l'expression du carré de la vitesse angulaire :

\theta'^{2}=\frac{3g}{L}(sin\theta_{0}-sin\theta)

Posté par
fidele11re : Tige homogène 29-05-21 à 18:02

Puisque ∅ varie en fonction du temps ;
la dérivée du carré de la vitesse angulaire est donc :
\frac{d\theta'^{2}}{dt}=\frac{-3g}{L}\theta'cos\theta

Posté par
vanoisere : Tige homogène 29-05-21 à 19:16

Il s'agit effectivement de dériver par rapport à t et non par rapport à ; ainsi :

\dfrac{d\left[\sin\left(\theta\right)\right]}{dt}=\dot{\theta}.\cos\left(\theta\right) comme tu l'as écrit mais aussi :

\dfrac{d\dot{\theta}^{2}}{dt}=2\dot{\theta}.\ddot{\theta}

Puisqu'il s'agit d'étudier un mouvement : \dot{\theta}\neq0 , ce qui permet une simplification...

Posté par
fidele11re : Tige homogène 29-05-21 à 20:55

Ok je vois, on peut donc égaliser les deux expressions,  simplifier ∅ comme vous l'avez dit et on a :

\theta''=\frac{3gcos\theta}{2L}

Posté par
vanoisere : Tige homogène 29-05-21 à 21:30

Bonne méthode mais problème de signe, me semble-t-il.

Posté par
fidele11re : Tige homogène 29-05-21 à 21:45

oups!
\theta''=-\frac{3gcos\theta}{2L}

Posté par
fidele11re : Tige homogène 29-05-21 à 21:45

oups!
\theta''=-\frac{3gcos\theta}{2L}

Posté par
fidele11re : Tige homogène 29-05-21 à 21:49

Pour l'accélération normale du point A, dois-je appliquer le TCI à la tige?

Posté par
vanoisere : Tige homogène 29-05-21 à 23:13

Inutile. Puisque le point A est animé d'un mouvement circulaire de centre O, l'accélération normale s'exprime simplement en fonction de L et du carré de la vitesse angulaire qui vient d'être étudié.

Posté par
fidele11re : Tige homogène 30-05-21 à 00:16

Donc c'est pareil à celle de la question 2.2) ?

Posté par
fidele11re : Tige homogène 30-05-21 à 19:00

Je parlais de cette expression :
a(n)=L∅'².

Posté par
vanoisere : Tige homogène 30-05-21 à 20:21

Je me demande s'il n'y a pas une faute de logique dans l'énoncé tel que tu l'as recopié. Logiquement, il s'agit à la question 3 de trouver l'accélération tangentielle en fonction de L et de l'accélération angulaire. Cette accélération tangentielle sera utile aux questions suivantes.

Posté par
fidele11re : Tige homogène 30-05-21 à 20:59

C'est ce que je me demandais aussi...

D'accord
puisque l'accélération angulaire et tangentielle de A (extrémité de la tige de longueur L ) sont liées par la relation a_{t}=L\theta'' ;
on a donc :
a_{t}(A)=-\frac{3}{2}gcos\theta .

Posté par
vanoisere : Tige homogène 30-05-21 à 21:33

D'accord.  N'oublie pas de préciser l'orientation de l'axe des z  avant de calculer la composante verticale de l'accélération du point A.

Posté par
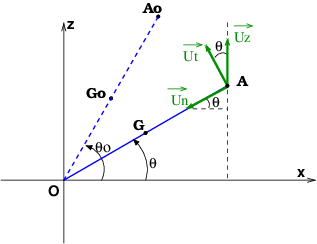
fidele11re : Tige homogène 30-05-21 à 23:06

voici comment je l'ai orienté (en image).


L'accélération az est :
\vec{a_{z}}=\vec{a_{n}}+\vec{a_{t}}
En norme:
a_{z}=\sqrt{a_{n}^{2}+a_{t}^{2}-2a_{n}a_{t}cosx} où x est l'angle entre l'accélération normale et tangentielle. x=π/2 rad
je reste avec a_{z}=\sqrt{a_{n}^{2}+a_{t}^{2}}

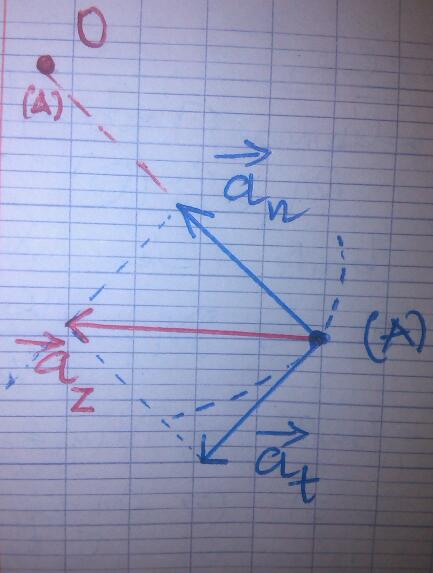
Tige homogène

Posté par
vanoisere : Tige homogène 31-05-21 à 15:15

Tu viens de déterminer la norme du vecteur accélération, ce vecteur accélération étant la somme vectorielle de l'accélération normale et de l'accélération tangentielle.
Relis bien l'énoncé : il s'agit de déterminer  la composante verticale az de ce vecteur accélération qui est la somme des composantes sur l'axe Oz de l'accélération normale et de l'accélération tangentielle :
az= anz + atz

Posté par
fidele11re : Tige homogène 31-05-21 à 20:21

J'oriente ainsi l'axe (Oz) suivant la direction de de l'accélération normale. Suivant cet axe, l'accélération tangentielle est nulle et le vecteur acceleration normal vaut -an=-3g(sin∅0 - sin∅).

Ainsi az=0- 3g(sin∅0 - sin∅)= 3g(sin∅0 - sin∅).

Pour ∅=∅0 => az=0

Posté par
vanoisere : Tige homogène 31-05-21 à 23:00

Non : relis bien l'énoncé ; l'axe (Oz) doit être vertical. Puisque l'angle est orienté vers le haut, tu as intérêt à orienter  l'axe (Oz) suivant la verticale ascendante.

Posté par
fidele11re : Tige homogène 01-06-21 à 07:24

Hmm je confonds déjà des choses..
En projetant l'acceleration normale sur cet (Oz) , je trouve qu'elle vaut ancosθ . De même, je trouve que l'acceleration tangentielle suivant (Oz) vaut -atcosα . avec α=π/2 - θ.

En faisant de ces accelerations et en remplaçant at et an par leurs expressions, je trouve:

a_{z}=3gcos\theta(sin\theta_{0} - sin\theta) - \frac{3}{2}gcos\thetasin\theta . Et lorsque θ=θ0 je reste avec az=-0,75gsin2θ

Posté par
vanoisere : Tige homogène 01-06-21 à 10:35

Tu pourrais commencer par faire une figure claire pour bien visualiser les projections. Je ne suis pas complètement d'accord avec ton calcul.

Posté par
vanoisere : Tige homogène 01-06-21 à 13:02

Ce schéma pourra peut-être t'aider...

Tige homogène

Posté par
fidele11re : Tige homogène 01-06-21 à 18:02

Ok Je trouve ceci:
a_{n}(z)=-a_{n}sin\theta ;
a_{t}(z)=a_{t}cos\theta
=> a_{z}= -a_{n}sin\theta+ a_{t}cos\theta

Posté par
vanoisere : Tige homogène 02-06-21 à 10:34

C'est bien cela. En remplaçant at et an par leurs valeurs, cela conduit à :

a_{z}=-3g.\sin\left(\theta\right).\left[\sin\left(\theta\right)-\sin\left(\theta_{o}\right)\right]-\frac{3}{2}g.\cos^{2}\left(\theta\right)

Posté par
fidele11re : Tige homogène 02-06-21 à 17:17

ok d'accord.
Lorsque ∅ est égale à ∅0 on a : sin∅=sin∅0
Ainsi sin∅-sin∅0=0
La valeur initiale de az est donc
=> a_{z}=-\frac{3}{2}gcos^{2}\theta .

5-condition pour que la bille quitte le godet dès le début du mouvement de la tige

Pour cela, je pense qu'il faut annuler l'accélération normale pour conserver l'accélération tangentielle. Cela me conduit à ∅=∅_0

Posté par
vanoisere : Tige homogène 02-06-21 à 19:43

Citation :
La valeur initiale de az est donc
=> a_{z}=-\frac{3}{2}g.\cos^{2}(\theta )=-\frac{3}{2}g.\cos^{2}(\theta_o) .

Pour bien comprendre imagine une bille de masse mb posée sur un plateau horizontal. L'ensemble est animé d'un mouvement vertical descendant d'accélération \vec a. Établis l'expression de la réaction \vec R que le plateau exerce sur la bille en fonction de mb, a et g. A quelle condition la bille reste-t-elle en contact avec le plateau ? Sinon elle décolle... Cela devrait t'aider...
Tu peux aussi, pour mieux comprendre réaliser l'expérience très simple suivante. Ta main à plat, bras tendu, remplace le plateau et tu places dans ta main un objet peu fragile (petite balle, bille...). Déplace ta main verticalement vers le bas avec une faible accélération puis abaisse brutalement ta main vers le bas pour lui communiquer une forte accélération vers le bas... Observe...

Posté par
fidele11re : Tige homogène 02-06-21 à 20:40

Pour le cas de la bille sur le plateau, on peut appliquer le théorème du centre d'inertie en supposant que nous sommes dans un référentiel galiléen. La bille étant soumise à son poids et à la réaction \vec{R} du plateau.
On a donc : \vec{P_b}+\vec{R}=m_{b}\vec{a} suivant le sens ascendant
-R+Pb=mba
<=> R=mb(g-a).
La bille reste collée au plateau si R existe. Dans le cas contraire, elle n'est plus en contact avec le plateau. Pour ce cas, R=0 => a=g.

Dans la deuxième expérience, je constate que l'objet se décolle de la main lorsque l'accélération de la main est grande et reste accolée pour une faible accélération.

Posté par
vanoisere : Tige homogène 02-06-21 à 21:18

Synthèse de ton calcul et des faits observés : la bille décolle pour :
a g.
Il te faut pour finir appliquer celà à ton problème.

Posté par
fidele11re : Tige homogène 02-06-21 à 22:12

Ok, la bille quitte le godet au début du mouvement (∅=∅_0) lorsque l'accélération initiale sur l'axe (Oz) est supérieure ou égale à g.
az≥g
suivant l'axe (Oz), le vecteur accélération g vaut -g
<=> -1,5gcos²(∅0)≥-g
g étant une constante positive non nulle :
<=>  cos(∅0)≤0,82
=> ∅0≤35,26°≈0,62 rad.

Posté par
vanoisere : Tige homogène 02-06-21 à 23:19

Attention : cos(x)=cos(-x). Il faut plutôt écrire :
-35,26°o35,26°

Ce résultat est assez logique intuitivement : pour que l'accélération initiale soit importante (supérieure à "g " en norme), la position initiale de la tige ne doit pas être trop écartée de l'horizontale.

Posté par
fidele11re : Tige homogène 02-06-21 à 23:52

D'accord bien noté.

Posté par
fidele11re : Tige homogène 02-06-21 à 23:55

Merci énormement à vous ..


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !