Inscription / Connexion Nouveau Sujet
Thévenin en régime sinusoïdale
Bonjour, je me pose une question quant a un exercice dont voici l'énoncé :
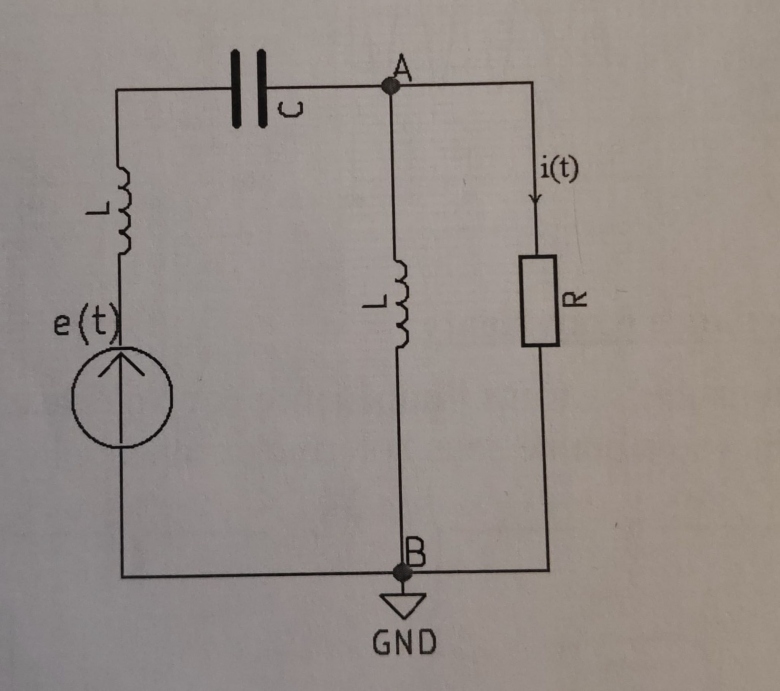
On considère le circuit suivant. Donner l'expression du courant complexe i(t) dans la résistance R. (Circuit en annexe)
Afin de calculer i(t) on fait d'abord Thévenin entre A et B pour avec la loi des mailles on retrouve i(t).
Lorsque l'on fait Thévenin, le prof nous a fait calculer directement VAB et ZAB sous forme complexe avec le module et l'argument avant de faire la loi des mailles pour trouver i(t). On a donc utilisé la loi des mailles avec les formes complexes de VAB et ZAB
Est-on obligé d'avoir ces formes complexes avant de faire cette lois des mailles ou alors peut on directement faire la lois des mailles avec les formules VAB et ZAB en fonction de e et des impédances ? Si ce n'est pas possible j'aimerais savoir pourquoi ?
J'ai fait les deux sortes mais je n'obtient pas le même résultat, lorsque je n'utilise pas VAB et ZAB sous forme complexe je n'ai pas les exponentielles avec l'argument dans la formule, mais à part ça i(t) à la même forme
Bonsoir
Les lois des mailles et des nœuds valides pour les tensions et les intensités instantanées , ainsi que les théorèmes divers démontrés pour ces valeurs instantanées (Thévenin, Norton, Millman...) sont aussi valides pour les complexes associées à ces grandeurs. Ensuite, pour chaque dipôle linéaire passif orienté en convention récepteur, tu poses :
u=Z.i
Tu reviens ensuite aux valeurs instantanées si nécessaire par la correspondance :
amplitude de la valeur instantanée = module du complexe associé
phase de la valeur instantanée = argument du complexe associé.
Concrètement : quel est le problème ici ? Tu peux exposer ici ta solution si tu as un doute.
Tu peux éventuellement aussi consulter la partie 1 du document référencé ici :
![]()
Aucun réel problème ici, je me demande simplement si il est possible d'arriver jusqu'à i(t) en gardant les expressions littérales non développés de Vab et Zab en fonction de Zc, Zl, etc. Ou si il est obligé de développer Vab et Zab afin de les mettre sous forme complexe pour arriver à i(t)
Je ne comprends pas bien ton problème. Pour arriver à i(t), il faut commencer à obtenir le complexe i et utiliser les règles de correspondance que j'ai rappelées dans mon message précédent.
Ceci étant dit, il y a plusieurs méthodes possibles pour arriver à i mais elles conduisent toutes aux même résultat.


