Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Thermodynamique : Théorème d'Archimède

Posté par
clauu 17-02-11 à 18:06

Voici l'énoncé :

On plonge un cylindre solide de diamètre d=8cm et de hauteur a=5cm ayant une densité ds=0,9 dans un réservoir cylindrique de diamètre D=10cm et de hauteur H=60cm contenant 1kg d'eau et 1kg d'huile de densité dh=0,75. Donner la position de la surface inférieure du solide dans le réservoir.

Voici ce que j'ai fait

On a donc deux phase.
Le Volume du petit cylindre : V = π r2 h soit V=251cm3
Le Volume du grand cylindre : W= 4712cm3

Veau= 1.103 cm3
Vhuile= (4/3).103 cm3

Les hauteurs des liquide dans le grand cylindre :

heau = Veau/ ( r2) = 12,73cm
Hhuile = Vhuile / ( r2) = 9,55cm

Comme dh<ds je considère que seul l'eau rentre en compte pour la somme des forces.

L'application de la seconde loi de newton donne : x la hauteur du petit cylindre immergé dans l'eau

= P
<=> eau x π r2 = s V
<=> x = ( s V ) / ( eau r2)
<=> x= 2,87cm

hsinf =heau-x = 9,86cm

Soit la surface inférieure du solide se trouve à 9,86 cm du fond du réservoir

Qu'en pensez vous?

Posté par
JEDarchimède 17-02-11 à 20:38

Bonsoir,

Etes vous sûr Hhuile ?

Comme dh<ds...............j'ai du mal à comprendre.

Voilà ce que je vous propose :

V1 volume dans l'eau.

V2 volume dans l'huile.

V = V1+ V2  volume du cylindre.
s(V1+v2) =eau*V1 + huile*V2

Donc V1 = V..............

Sur le plan numérique je ne suis pas loin de votre résultat.

A vous lire.  JED.

Posté par
clauure : Thermodynamique : Théorème d'Archimède 18-02-11 à 12:27

Citation :
dh<ds
= densité de l'huile inférieure a la densité du solide ( petit cylindre ) donc je peux négliger l'effet de l'huile non ?

Citation :
V1 volume dans l'eau.

V2 volume dans l'huile.

V = V1+ V2  volume du cylindre.


Il n'est pas dit que le cylindre est remplis a ras bord par les liquides seulement qui les contient donc sa marche pas, non?

Posté par
Marc35re : Thermodynamique : Théorème d'Archimède 20-02-11 à 13:09

Bonjour,

Citation :
= densité de l'huile inférieure a la densité du solide ( petit cylindre ) donc je peux négliger l'effet de l'huile non ?

Non, certainement pas !...
Si dh < ds, la force d'Archimède existe, même si elle est plus faible que le poids de l'objet.

Posté par
clauure : Thermodynamique : Théorème d'Archimède 20-02-11 à 16:27

Citation :
Non, certainement pas !...
Si dh < ds, la force d'Archimède existe, même si elle est plus faible que le poids de l'objet


Je fais comment alors ??
Dans Mon bilan des forces?

F =  - eau - huile + P = 0

donc P = eau + huile  ??
C'est sa?

Posté par
Marc35re : Thermodynamique : Théorème d'Archimède 20-02-11 à 17:57

Oui, c'est ça...

Posté par
J-Pre : Thermodynamique : Théorème d'Archimède 20-02-11 à 18:26

Après quelques calculs , le cylindre aura sa partie inférieur dans l'eau et sa partie supérieure dans de l'huile et sera complètement immergé.

Soit h1 la hauteur du cylindre dans l'eau.
soit h2 = 0,05 - h1 la hauteur du cylindre dans l'huile.

Pa(huile) = Pi.d²/4.h2.Rho huile.g
Pa(eau) = Pi.d²/4.h1.Rho eau.g

Pa(totale) = Pi.d².g/4 * (h2.Rho huile + h1.Rho eau)
Pa(totale) = Pi.d².g/4 * ((0,05-h1).Rho huile + h1.Rho eau)
Pa(totale) = Pi.d².g/4 * ((0,05-h1).750 + h1.1000)

Poids cylindre = Pi.d²/4.a.g * Rho cyl
Poids cylindre = Pi.d²/4.0,05.g * 900

Le cylindre flotte et donc Pa(totale) = Poids cylindre --->
Pi.d².g/4 * ((0,05-h1).750 + h1.1000) = Pi.d²/4 *0,05.g * 900

(0,05-h1).750 + h1.1000 = 0,05 * 900
250 h1 = 45 - 37,5
h1 = 0,03 m = 3 cm
---
Volume d'eau + Volume de 3 cm de haut du cylindre = 10^-3 + Pi.0,05²/4 * 0,03 = 0,0010589 m³ = 1058,9 cm³

Niveau de l'eau dans le cylindre :  1058,9/(Pi*10²/4) = 13,48 cm
---
Le fond du cylindre est 13,48 - 3 = 10,48 cm plus haut que le fond du réservoir
-----

Aucun calcul vérifié.  

Posté par
clauure : Thermodynamique : Théorème d'Archimède 21-02-11 à 17:45

Citation :
Volume d'eau + Volume de 3 cm de haut du cylindre = 10^-3 + Pi.0,05²/4 * 0,03 = 0,0010589 m³ = 1058,9 cm³

Niveau de l'eau dans le cylindre : 1058,9/(Pi*10²/4) = 13,48 cm
---
Le fond du cylindre est 13,48 - 3 = 10,48 cm plus haut que le fond du réservoir



le diamètre du petit cylindre est d=8cm =>le rayon r= 4cm

Veau+Vvolume immergé dans l'eau = 1.103 + 342
Veau+Vvolume immergé dans l'eau 1150,79

H= ( Veau+Vvolume immergé dans l'eau ) / ((10/2)2)
H14,65

Hinf = H- hs1
Hinf = 14,65-3
Hinf = 11,65 cm

Le petit cylindre est à environs 11,65 cm du fond du grand cylindre

Qu'en pensez vous?

Posté par
Marc35re : Thermodynamique : Théorème d'Archimède 22-02-11 à 13:18

Pour moi, il faut résoudre ce problème en essayant de simplifier au maximum les calculs c'est-à-dire ne pas se lancer "bovinement" dans les calculs avec des arrondis partout qu'on ne maîtrise pas...
Le cylindre ne flotte pas dans l'huile, il coule jusqu'à l'eau. Dans l'eau, il flotte. Il se stabilise à une position d'équilibre à la limite de l'huile et de l'eau dans laquelle s'exercent trois forces : le poids, la force d'Archimède due à l'huile et la force d'Archimède due à l'eau.
(Le schéma n'est pas à l'échelle)
On va calculer la hauteur d'eau dont on aura besoin ensuite.
1 kg d'eau ==> 10-3 m3
3$V_e\,=\,\pi\,\frac{D^2}{4}\,h_e\,\Rightarrow\,h_e\,=\,\frac{4V_e}{\pi D^2}
3$h_e\,=\,\frac{4.10^{-3}}{\pi (10^{-1})^2}\,=\,\frac{4}{\pi}\,10^{-1}\,\simeq\,0,127\,\,m\,=12,7\,\,cm\,
\mu_h  est la masse volumique de l'huile,  \mu_e  est la masse volumique de l'eau et  \mu_s  est le masse volumique du cylindre.
Force d'Archimède due à l'huile
3$F_h\,=\,\mu_h\,\pi\frac{d^2}{4}\,(a-x)\,g
3$d_h\,=\,\frac{\mu_h}{\mu_e}\,\Rightarrow\,F_h\,=\,d_h\mu_e\,\pi\frac{d^2}{4}a\,g\,-\,d_h\mu_e\,\pi\frac{d^2}{4}x\,g
Force d'Archimède due à l'eau
3$F_e\,=\,\mu_e\,\pi\frac{d^2}{4}\,x\,g
Poids du cylindre
3$P\,=\,\mu_s\,\pi\frac{d^2}{4}\,a\,g\,=\,d_s\,\mu_e\,\pi\frac{d^2}{4}\,a\,g
En projetant sur un axe orienté vers le bas (par exemple)
3$P\,-\,F_h\,-\,F_e\,=\,0
3$d_s\,\mu_e\,\pi\frac{d^2}{4}\,a\,g\,-\,d_h\mu_e\,\pi\frac{d^2}{4}a\,g\,+\,d_h\mu_e\,\pi\frac{d^2}{4}x\,g\,-\,\mu_e\,\pi\frac{d^2}{4}\,x\,g\,=\,0
3$\mu_e\,\pi\frac{d^2}{4}\,g\,(d_sa\,-\,d_ha\,+\,d_hx\,-\,x)\,=\,0
3$d_sa\,-\,d_ha\,+\,d_hx\,-\,x\,=\,0

3$a(d_s-d_h)+x(d_h-1)\,=\,0
D'où :
3$x\,=\,a\,\frac{d_s-d_h}{1-d_h}
Application numérique :  3$x\,=\,3\,\,cm
D'où la position de la surface inférieure du solide dans le réservoir :
3$h_e\,-\,x\,=\,\frac{4}{\pi}\,10^{-1}\,-\,3.10^{-2}\,=\,9,7\,\,cm

sauf erreur éventuelle...
Calculs à reprendre entièrement bien entendu...

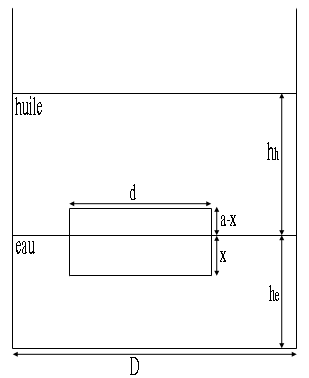
Thermodynamique : Théorème d\'Archimède

Posté par
J-Pre : Thermodynamique : Théorème d'Archimède 22-02-11 à 14:57

Pas d'accord avec les calculs de Marc35.

he n'est pas correct.

Ce qui impose he vient du volume d'eau mais aussi de la partie du cylindre de hauteur x.
-----
Voir ma première réponse (en corrigeant le diamètre erroné que j'avais utilisé).


Volume d'eau + Volume de 3 cm de haut du cylindre = 10^-3 + Pi.0,08²/4 * 0,03 = 0,0011508 m³ = 1150,8 cm³

Niveau de l'eau dans le cylindre : 1150,8/(Pi*10²/4) = 14,65 cm
-----
Le fond du cylindre est 14,54 - 3 = 11,65 cm plus haut que le fond du réservoir

Sauf nouvelle distraction.  

Posté par
clauure : Thermodynamique : Théorème d'Archimède 22-02-11 à 16:23

C'est bien ce que j'ai trouvé en remplaçant le he = 12,7 que suggéré Marc35 par la hauteur de l'eau en prenant en compte le volume du cylindre...

Merci beaucoup à vous deux

Posté par
Marc35re : Thermodynamique : Théorème d'Archimède 22-02-11 à 16:33

Ah oui, exact...Désolé. Il faut tenir compte de la partie du cylindre immergée pour la hauteur d'eau...
Il faut penser à tout !

Posté par
clauure : Thermodynamique : Théorème d'Archimède 23-02-11 à 21:01

pouvez vous jeter un coup d'oeil sur ce topic s'il vous plait https://www.ilephysique.net/sujet-thermodynamique-forces-de-pression-246536.html
Merci d'avance


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !