Inscription / Connexion Nouveau Sujet
Thermodynamique : Forces de Pression
Énoncé
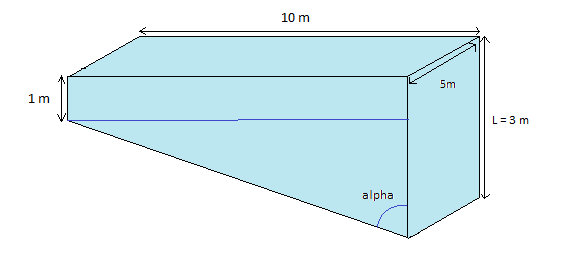
Déterminer la résultante des forces de pression qu'exerce l'eau d'une piscine de 10m sur 5m sur le fond lorsque la profondeur varie linéairement de 1 m à 3m
Ce que j'ai fait
J'ai considéré deux niveaux, le premier est le pavé droit 1 10
10 5
5
et le prisme droit à base triangulaire 3 10
10 5
5
Je calcule la Pression à 1m de profondeure => P1 = Path + 
 g
g h1
h1
avec h1 la profondeur c.à.d 1m
Ensuite je calcule la pression sur le fond de prisme
P(h) = P1+
 g
g h
h
Toujours dans le prisme on à alors
dS = L (dh/cos )
)
dFs = P dS
dS
dFs = [P1+
 g
g h]
h] L (dh/cos
L (dh/cos )
)
Au final en intégrant dF :
 (dFs) = (L/(cos
(dFs) = (L/(cos ))
)) (Path+
(Path+
 g(h1+(1/2)h))h
g(h1+(1/2)h))h
J'ai donc
Fx= L (Path+
(Path+
 g(h1+(1/2)h))h
g(h1+(1/2)h))h
Fy= -L tan
tan
 (Path+
(Path+
 g(h1+(1/2)h))h
g(h1+(1/2)h))h
J'ai peur de mettre embrouillé dans mes hauteurs
Qu'en pensez vous?
le prisme droit à base triangulaire 3 10
10 5 ==> 2
5 ==> 2 10
10 5 à mon avis
5 à mon avis
dS = L (dh/cos ) ==> oui si L = 5 m (sur le schéma L = 3 m)
) ==> oui si L = 5 m (sur le schéma L = 3 m)
A part ça, je suis d'accord avec le résultat final (pour l'application numérique, il faut intégrer h de 1 à 3 sauf erreur de ma part).
oui c'est une erreur du schéma L= 5 m
Vous pensez qu'il faut une application numérique ???
Je pensais qu'il ne valait que des expressions...
comme h est a partir de -1m à partir de la surfac
si xo = 0 est la surface de la psicine...
h = x0-h1 ???
Je ne sais pas... Ce n'est pas précisé dans l'énoncé (sauf s'il n'est pas complet)...
Mais, si on donne les valeurs numériques, ce n'est pas par hasard sans doute. Sinon il n'est pas nécessaire de préciser les dimensions numériquement mais je ne peux pas assurer qu'il faut faire l'application numérique.
En toute rigueur, ce n'est pas explicitement demandé mais...
Le plus simple est d'orienter l'axe vers le bas avec le 0 à la surface de la piscine mais on doit y arriver avec un axe orienté vers le haut aussi (on a des h négatifs).
Si si l'énoncé est complet ..
c'est ce que j'aurai fait un axe vers le haut
avec xo=0 la surface de l'eau de la piscine
Il faut donc intégré de -1 à -3...
je viens de regarder mon cour...
dans
PB = PA + 
 g
g h
h
h est toujours positif car c'est un distance
on a fait un exemple avec un plongeur qui descend a 20m, et dans la formule de l'application on a h = 20 et non h=-20
Donc sa marche...
Dans ce cas il faut intégré h de 0 à 2 alors ...
Puisque à 1 métre de profondeur :
P(h) = P1 + 
 g
g h
h
le h de la formule = 0 non?
Oui, h de 0 à 2, je suis d'accord...
6 047 250 N, c'est le poids d'une masse de 604 725 kg environ, soit 605 tonnes environ
Hum !!...ça fait beaucoup mais l'eau, c'est très lourd...
1 L d'eau a une masse de 1 kg. Donc 1 m3 (==> 1000 fois plus) a une masse de 1000 kg soit 1 tonne.
Si on prend simplement la partie du haut (h = 1 m), V = 10 5
5 1 = 50 m3 donc 50 tonnes.
1 = 50 m3 donc 50 tonnes.
Si on prend un parallélépipède de 10 m sur 5 m et 3 m de haut (donc sans plan incliné), V = 10 5
5 3 = 150 m3 donc 150 tonnes.
3 = 150 m3 donc 150 tonnes.
Donc 600 tonnes, ça a l'air de faire beaucoup effectivement.
J'ai beau refaire les calculs
je tombe encore et encore sur ces résultats...
mais on doit forcément obtenir un résultat de l'ordre de
Puisque Path 10
10  106
106


