Niveau maths sup

Thermodynamique et Pression

Posté par
miss-laure 03-04-10 à 16:11

Bonjour

Je voudrais solliciter votre aide à propos d'un exercice de thermodynamique dont voici l'énoncé :

Un hémisphère creux est en contact suivant un cercle de rayon R avec un plan horizontal. Celui ci est relié à une pompe à vide destinée à rendre la pression intérieure très faible (négligeable devant la pression atmosphérique P0)
Exprimer en fonction de P0 et R, la force qu'un opérateur doit exercer sur la poignée de l'hémisphère pour le soulever

En fait, je connais la relation dF=P*dS*n avec F et n vecteurs
mais je me demande si je dois utiliser un repère polaire ou sphérique car on me parle de sphère et de cercle :S
Auriez vous le temps de m'expliquez pas à pas la démarche à suivre ?

en vous remerciant de votre patience, Laure.

Posté par Calcul de force 03-04-10 à 18:47

Bonsoir laure,

Ici, tu as deux voies. Soit tu pars d'un élément de surface en coordonnée sphérique et tu calcules $\vec{F}=\iint_S P_0.\vec{dS}$ (intégrale fermée mais il ne semble pas connaitre \oiint). Mais, cela demande un certains bagage mathématiques dont j'ignore l'étendue en ce qui te concerne.

Soit, la voie que je te recommande pour aller vite. A partir d'une décomposition astucieuse de $\vec{dF}$ et d'argument du symétrie, tu peux donner le sens et la direction de F ainsi que $||\vec{dF}||$ et ainsi réduire le calcul à une intégrale simple.

Je suis resté évasif pour que tu puisses chercher un peu mais si tu bloques toujours, dis le, on t'aidera de manière plus explicite.

Bonne chance.
BS

Posté par Pression sur une demi sphère 04-04-10 à 21:37

Bonsoir BS

D'abord Merci pour votre réponse

J'ai étudié les deux solutions que vous m'avez exposées. La première ne m'est pas accessible car calculer une intégrale fermée est apparemment étudiée en seconde année, or je ne suis qu'en première année. Je me suis donc tournée vers votre deuxième proposition.

Malheureusement, celle ci ne semble pas plus m'éclairer, je pourrais commencer par réduire le demi cercle de moitié et ne garder donc qu'un quart du cercle entier ( selon votre proposition d'élements de symétrie) Je sais que le poids est une force qui agit selon une verticale.
je peux considerer qu'une demi-sphere est un empilement de disques de diametre décroissants.
alors si j'etudie un disque en particulier , il va etre soumis a la pression sur sa tranche. ainsi la pression totale est la somme de celle exercée sur chaque tranche

A partir de ça, je suis perplexe :s

Bonne soirée, Laure.

Posté par Force de pression 04-04-10 à 22:52

Bonsoir laure,

En effet, la première n'est pas à ta portée. Non pas pour l'intégrale double (qui peut être à niveau maths-sup si on admet le Th. de fubini. Le problème est surtout l'intégration du vecteur unitaire Ur. Et là, ça demande un peu de pratique.

PS : On travaille en coordonnée sphérique.

Donc, on se cantonne à l'analyse des symétries. L'idée, est de trouver le valeur de $\vec{dF_C}$ , un élément de force pour un élément de surface engendré par la rotation suivant phi. On v

Posté par Force de pression 04-04-10 à 23:07

Et on recommence...

Bonsoir laure,

En effet, la première n'est pas à ta portée. Non pas pour l'intégrale double (qui peut être à niveau maths-sup si on admet le Th. de fubini. Le problème est surtout l'intégration du vecteur unitaire Ur. Et là, ça demande un peu de pratique.

PS : On travaille en coordonnée sphérique.

Donc, on se cantonne à l'analyse des symétries. L'idée, est de trouver le sens et la direction de $\vec{F}$ . Je te propose de travailler suivant une coupe de la demi-sphère passant par le centre de sphère associée. On obtient le schéma suivant dans le plan (0,x,Uy)

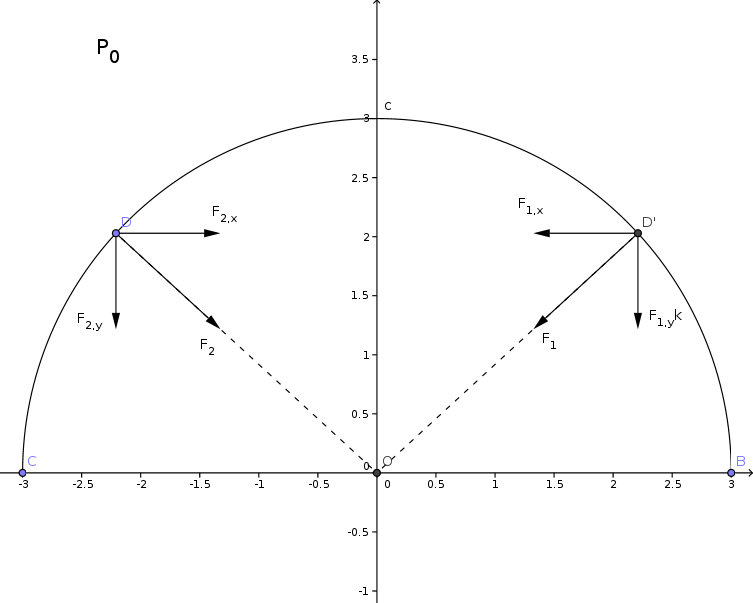
Force de pression

Vu que Po est constant (d'un par car l'altitude est la même et aussi car pour cette variation d'altitude, on pourrait approximer P comme constante), on peut dire que $\vec{F_{2,x} = -\vec{F_{1,x}$ car $\widehat{DOC} = \widehat{D'OB}$ car D' est le symétrique de D par rapport à (O,Uy). Ainsi, on peut dire que la résultante $\vec{F}$ est colinéaire à Uy ou dans le repérage sphérique en Ur. Maintenant, tu peux intégrer puisque l'on a levé la difficulté vectorielle.

J'aimerais que tu essayes de l'intégrer seule.

Bonne chance.
BS

Posté par pression sur une demi sphère 07-04-10 à 18:05

Bonjour BS,

j'ai compris votre dernier message et j'ai intégré ! Voici ce que ça donne :

dF=P0*dS*n
or dans le repère sphérique, dS=R²sindd
alors dF=P0 R² sin cos dd

alors F=P0 R² sin cosdd
on intégre entre 0 et 2 et entre 0 et /2 car symétrie que vous m'avez expliqué

on obtient F= P0 R² [-1/2cos²] []

et donc F= P0*R²*

voila ce que j'ai réussi à faire, qu'en pensez vous? la solution est elle correcte ??

Merci beaucoup BS de votre temps, Amitiés, Laure

Posté par Thermo 07-04-10 à 21:27

Bonsoir Laure,

C'est un plaisir avec des élèves qui cherche.

Pour ta proposition. L'idée est là et le résultat est juste. Par contre, la rédaction et les justifications sont mauvaises.
(As tu eu une autre correction ?)

On travaille dans deux repères. Le premier est (O,Ur,Ut,Up) en coordonnée sphérique et la second est (O,Ux,Uy,Uz) en coordonnée cartésienne.

On sait que :
$\vec{dF} = P_0.\vec{dS}$ .
Grâce au dessin, on a montré que seule la composante selon z est contributive à la force pressante exercée sur la sphère et quelle est orienté suivant -Uz. Donc, $\vec{dF} = -P_0.\cos(\theta).dS.\vec{U_z}$ . Sachant que le cosinus provient de la projection de $\vec{dF}$ sur z.

Maintenant, que l'on a le vecteur r exprimer sur une base cartésienne, on peut intégrer (car les vecteurs unitaires cartésiens sont constants dans ce repère).

Donc,

$\vec{F} = \iint_S P_0.\vec{dS} = -\iint_S P_0.dS.\vec{U_z}$
En utilisant les coordonnées sphériques sur dS, on a : $\vec{F} = -P_0.\int_{0}^{\pi}\int_{0}^{2\pi} r^2.\cos(\theta).\sin(\theta).d\theta.d\phi$ (Je te rappelle que l'ordre des d est celui des intégrales. Cette intégrale peut s'écrire grace au Th. de Fubini comme :

$\vec{F} = -P_0.r^2.\int_{0}^{\frac{\pi}{2}}\cos(\theta).\sin(\theta).d\theta.\int_{0}^{2\pi}d\phi$
$\vec{F} = -P_0.r^2.\frac{1}{2}.(\sin^2({\frac{\pi}{2}})-\sin^2(0)).2\pi$
$\vec{F} = -P_0.r^2.\frac{1}{2}.2\pi = -\pi.r^2$

CQFD.

PS : Les bornes d'intégrations ne viennent pas de la symétrie, c'est pour prendre en compte l'ensemble de la demi sphère.

Pour le fun, je te montre sans argument de symétrie.

$\vec{F} = \iint_S P_0.\vec{dS} = \iint_S -P_0.dS.\vec{U_r}$ (Car la force vient de l'extérieur).
$\vec{F} = \iint_S -P_0.\vec{dS} = \iint_S -P_0.dS.(\sin(\theta).\sin(\phi).\vec{U_x} + \sin(\theta).\cos(\phi).\vec{Uy} + \cos(\theta).\vec{U_z})$
$\vec{F} = \iint_S -r^2.P_0.(\sin(\theta).\sin(\phi).\vec{U_x} + \sin(\theta).\cos(\phi).\vec{Uy} + \cos(\theta).\vec{U_z}).\sin(\theta).d\theta.d\phi$
$\vec{F} = -r^2.P_0.(\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\pi} \sin^2(\theta).\sin(\phi).d\theta.d\phi.\vec{U_x} + {\frac{\pi}{2}}\int_{0}^{2\pi} \sin^2(\theta).\cos(\phi).d\theta.d\phi.\vec{Uy} + \int_{0}^{\frac{\pi}{2}}\int_{0}^{2\pi} \cos(\theta)\sin(\theta).d\theta.d\phi.\vec{U_z})$
$\vec{F} = -r^2.P_0.(\int_{0}^{\frac{\pi}{2}}\sin^2(\theta).d\theta.\int_{0}^{2\pi} \sin(\phi).d\phi.\vec{U_x} + \int_{0}^{\frac{\pi}{2}} \sin^2(\theta).d\theta.\int_{0}^{2\pi}\cos(\phi).d\phi.\vec{Uy} + \int_{0}^{\frac{\pi}{2}}\cos(\theta)\sin(\theta).d\theta.\int_{0}^{2\pi} d\phi.\vec{U_z})$

Or les intégrales sur leurs périodes de cos et sin en phi annulent les intégrales suivant les vecteurs Ux et Uy. En conséquence, on retrouve bien.

$\vec{F} = -P_0.r^2.\int_{0}^{\frac{\pi}{2}}\cos(\theta).\sin(\theta).d\theta.\int_{0}^{2\pi}d\phi$
qui suit le même calcul.

Voila de quoi te régaler.

Si tu as d'autres questions.

PS : Normalement, ça doit aller mais en Latex, il se peut que je laisse passer des erreurs d'étourderies dans les calculs.

Cordialement.
BS