Inscription / Connexion Nouveau Sujet
thermodynamique
bonjour à tous,
j'etudie actuellement la thermodynamique. C'est loin d'être une chose aisée.
J'ai quelques soucis avec les exercices. je vous le met a la suite.
Un réservoir de grande capacité contient de l'air à la pression relative de 6 bar et à une température égale à 20°C. Cet air est utilisé pour regonfler un pneumatique sans chambre, de volume supposé constant, initialement à 20°C et à la pression relative de 1.2 bar.
Hypothèse : l'air se comporte comme un mélange de gaz parfait.
Données : - capacité calorifique molaire à pression constante de l'aire dans le domaine de l'étude : 29.2 J·mol-1·K-1 ;
- volume interne du pneumatique : 0.02m3 ;
- pression atmosphérique : 105 Pa.
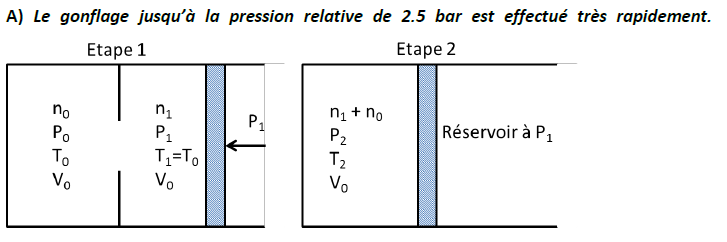
A) Le gonflage jusqu'à la pression relative de 2.5 bar est effectué très rapidement.
voir schema.
1) En sachant que le gonflage est très rapide, caractériser la transformation (isotherme, isochore, isobare, adiabatique ?).
2) Ecrire la variation de l'énergie interne de ce système fermé (ΔUn0+n1) et l'exprimer en fonction des températures.
3) La grande capacité du réservoir permet de considérer que la pression qui y règne, P1, n'est pas affectée par le départ des n1 moles de l'air. Ecrire donc l'échange de travail par ce système avec les forces extérieures.
4) Appliquer le premier principe de thermodynamique au système et utiliser les réponses 2) et 3) pour l'exprimer en termes des variables {P,V,T}.
5) Quelle sera la température de l'air contenu dans le pneumatique (T2) à la fin de ce gonflage rapide ? Application numérique.
B) La valve étant refermée, l'air se met ensuite en équilibre thermique avec son environnement dont la température est égale à 17°C. Calculer :
a) la pression à l'intérieur du pneumatique. Application numérique.
b) la quantité de chaleur échangée par l'air lors du cette seconde étape. Application numérique.
Pour la premiere question, qu'est ce qu'il entend par caracterisé? Il faut juste dire quelle est la nature de la transformation (isochore, isobare...)? D'apres le schema seul le volume reste consant, en plus c'est ecrit volume supposé constant. Mais est ce que je dois me contenter de cette reponse ou je doit faire une demonstration mathematique?
2eme question: Pour la variation d' energie interne est ce que je peut utiliser U= 3/2nRT? ce qui me ferait Uf-Ui = 3/2nRTf -3/2nRTi = 3/2nR(TF-TI) où n vaut n1+n0??
3e question: si je ne dis pas de betise, Pext 10^5 Pa, P1 c'est la pression dans le reservoir (6bar), P0 est la pression dans le pneu 1.2 bar et P2 la pression a la fin du gonflage? ici c'est une transformation rapide, donc elle n'est pas quasi statique. donc on a W= -Pext.(Vf-Vi)
Merci pour votre aide parce que la je rame pas mal
Bonjour
Si je comprends bien l'énoncé, il s'agit de se ramener à l'étude d'un système fermé en choisissant comme système les (n0+n1) moles de gaz, comme suggéré par le schéma.
Il faut savoir que les échanges thermiques sont toujours des phénomènes très lents. Considérer que le gonflage est très rapide revient donc à considérer cette étape comme adiabatique. Attention : la structure à gonfler est de volume fixe mais le système des (n0+n1) moles de gaz ne subit pas une évolution isochore.
La question 2 revient effectivement à utiliser la première loi de Joule. Attention : l'air n'est pas assimilable à un gaz parfait monoatomique comme tu l'écris. La capacité calorifique molaire à volume constant se déduit de la capacité calorifique molaire à pression constante (valeur fournie) par utilisation de la relation de Mayer.
Pour la question 3 : conformément au schéma, on peut calculer le travail reçue par le système en considérant que les n1 moles sont "poussées" à pression constante (7bars) dans la structure gonflable par le reste du gaz du réservoir.
Attention : la pression atmosphérique vaut 1bar et toutes les données sont en pression relatives alors que les lois de la thermodynamique utilisent les pressions absolues : (pression relative+ pression atmosphérique).
Je te laisse réfléchir à tout cela et proposer un début de solution.
bonjour,
merci pour votre aide.
Donc pour la question deux, gaz diatomique l'energie interne est U= CvT avec Cv= 5/2nR
on a donc un DU= 5/2nR (Tf - Ti) ?
Attention : il se raconte pas mal de bêtises à propos de ce problème par ailleurs... On se comprends j'espère... Il faut s'inspirer du schéma fourni en bas d'énoncé et choisir comme système les (n1+n0) moles de gaz, le reste du réservoir de gaz agissant comme un piston qui exercerait sur le système la pression fixe de 7bars. (Raisonner en pression absolue)
C'est vrai que pour un gaz parfait diatomique, la capacité calorifique molaire isochore est égale à (5R/2) mais ici, je pense qu'il faut utiliser la relation de Mayer puisque la valeur numérique de Cpm est fournie : 29,2J.K-1.mol-1 :
Cvm=Cpm - R
La variation d'énergie interne du système est donc ainsi :
 U=(n1+n0).Cvm.(T2-T0)
U=(n1+n0).Cvm.(T2-T0)
Puisque Q=0, Tu peux ensuite écrire :
 U=W
U=W
ce qui te donnera l'élévation de température. W est le travail fourni par le reste du gaz du réservoir qui agit comme un piston exerçant la pression fixe de 7bars.
je viens de comprendre, j'avais un petit soucis avec cette relation de mayer, car dans mon cours c'est cp-cv=nR, mais on parle en capacité calorifique thermique. et non molaire, d'ou le n qui apparait. (si je ne dit pas de betise).
donc j'ai bien Cmp - Cmv= R d'ou Cmv = Cmp - T ok
energie intern pour une transformation adiabatique (desole je ne sais pas faire le triangle) DU = nCvmDT donc = (n1+n0). (Cmp - R) (T2 - T0) (1)
comme j'ai DU= W alors W= (1)
soit (T2-T0) = W/ ((n1+n0).(Cmp - R))
pour ce genre de tranformation W = -P (Vf-Vi) ou P =pression absolue de 7bar ?
mais quel sont mes valeurs de Vf et Vi ? on garde juste V0? donc W= -PV0??
Tout est sur le schéma : le volume du système passe de 2Vo à Vo. Attention W>0 : le gaz du réservoir fournit une poussée sur le système et donc le travail est moteur. La formule classique conduit d'ailleurs à une valeur positive :
W=-P1.(Vf - Vi)=-P1.(Vo-2Vo)=P1.Vo
bien sur, logique, mon erreur, j'etait pas sur le 2V0
donc je finis avec DT = P1.Vo/((n1+n0).(Cmp - R)) ?
Non !
 U=W
U=W
(no+n1)Cpm(T2-To)=P1.Vo
Sachant que le gaz vérifie l'équation d'état des gaz parfaits... Ne pas oublier que l'énoncé fournit les pressions relatives !
Je te laisse déterminer T2.
j'etait en train de faire la correction, vu qu'on me demande la variation de l'energie interne donc forcement DU. c'est parce que je me perd un peu dans tout ces exercices.
grosso modo mes reponse c'est (je vais develloper sur ma copie)
question 2 :
DU=(n1+n0).Cvm.(T2-T0)
question 3
W=P1.V0
question 4 on applique le 1er principe donc
DU=W
soit (no+n1)Cpm(T2-To)=P1.Vo
question 5 application numerique, je trouve T2
je suis pas certains, je pense que j'ai oublier un truc quelques part
Je crois bien que je t'ai fourni un résultat faux, en me laissant induire en erreur par le schéma fourni en fin d'énoncé qui en réalité est faux : selon ce schéma, les n1 moles de gaz occupent sous la pression P1 un volume Vo. Cela n'est pas écrit dans l'énoncé et se révèle en fait faux. Heureusement, cela ne change pas le raisonnement mais modifie l'expression de W puisque le volume passe maintenant de (Vo+V1) à Vo. Il faut donc poser :
 U=W
U=W
(no+n1)(Cpm-R)(T2-To)=P1.V1
Cela donne une équation avec deux inconnues : T2 et V1. On obtient une seconde équation en appliquant la loi des gaz parfaits au système en fin de gonflage, avant refroidissement :
(no+n1)RT2=P2.Vo
Sauf erreur de calcul toujours possible de ma part, cela conduit à :
T2=327,8K et V1=2,66.10-3m3
Contrairement au schéma fourni : Vo V1 !
V1 !
bonjour,
effectivement il y avait une erreur sur le poly.
Par contre je ne comprend pas comment tu arrive de
(no+n1)(Cpm-R)(T2-To)=P1.V1
à
(no+n1)RT2=P2.Vo
Il suffit de reprendre mon raisonnement du 11-03-19 à 14:09 en appelant V1 et non Vo le volume des n1 moles de gaz à la pression P1 :
le volume du système passe de (Vo+V1) à Vo. Attention W>0 : le gaz du réservoir fournit une poussée sur le système et donc le travail est moteur. La formule classique conduit d'ailleurs à une valeur positive :
W=-P1.(Vf - Vi)=-P1.(Vo-Vo-V1)=P1.V1
Ensuite :
 U=W
U=W
....
Regarde le schéma de droite qui lui est correct : en fin de gonflage, les (n1+no) moles sont à la température T2, sous la pression P2=3,5bars en occupant le volume Vo. Équation d'état des gaz parfaits...
Pour terminer le problème, tu peux aussi écrire :
no.R.To=Po.Vo
n1.R.To=P1.V1
ha ben ui, jsuis a cote de la plaque aujourd'hui dsl pv=nrt . desolé merci pour ta patience
je reviens des que j'ai T2
Je vais t'aider un peu pour obtenir T2 car ce problème n'est effectivement pas très simple. Il suffit en fait d'utiliser les deux formules que nous avons obtenues en remplaçant no et n1 par leurs expressions déduites de l'équation d'état des gaz parfaits. Cela donne un système de deux équations à deux inconnues : V1 et T2.
Une fois simplifié, ce système conduit à : T2 = 327,8K ; V1 = 2,66.10-3m3
je seche quand meme. J'ai beau retourner dans tout les sens pas moyen d'extraire l'un ou l'autre.
J'arrive a avoir T2 en fonction de V1 et V1 en foction de T2 mais derriere des que j'essaie de remplacer un terme dans une equation soit je fait une boucle pour rien, soit je me retrouve avec une equation d'1km impossible a simplifier pour l'application numerique
C'est effectivement un peu délicat si tu cherches à résoudre littéralement. Tu peux sans doute remplacer toutes les grandeurs connues par leurs valeurs numériques. Tu obtiens alors un système assez simple de deux équations à deux inconnues.


