Inscription / Connexion Nouveau Sujet
Thermodynamique
Bonjour, j'aurai besoin de votre aide sur un exercice de thermodynamique, voici le sujet :
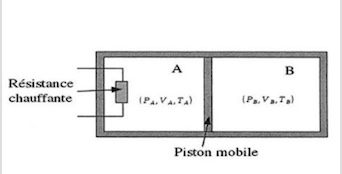
Soit un cylindre contenant un gaz parfait diatomique au parois calorifugées et indéformables, séparé par un piston mobile ( sans frottement ) lui même calorifugé. A l'état initial, les deux parties du cylindre A et B se trouvent dans les même conditions d'état ( Po, Vo, To no=1mol )
On chauffe lentement la partie A à l'aide d'une résistance chauffante jusqu'à PAf = 5Po. Dans tout ce qui suit, les calculs se feront en fonction des paramètre initiaux.
1) Dans quel sens va se déplacer le piston ? Justifier sans calculs
Le piston se déplace vers la droite car lorsque on chauffe la partie A la pression final PAf est de 5Po
2) Quel type de transformation subit le gaz dans la partie B ? Justifier sans calculs
Le gaz dans la partie B subit une transformation réversible adiabatique car dans l'énoncé on nous dit " On chauffe lentement la partie A "
3) Donner la relation qui relie les paramètre d'état pour cette transformation ?
PoVo^\gamma = PfVf^\gamma
4) Déterminer tout les paramètres d'état pour les deux parties A et B à l'état d'équilibre final
-PAf = 5Po
-VAf = ( (PoVo^
)/ PAf )1/
TAf= PAfVAf/ nR
- PBf = je ne sais pas
- VBf = ( (PoVo^\ )/ PBf )1/
- TBf= PBfVBf/ nR
Que vaut la variation d'énergie pour le système global A+B ?
U = 
Q +W
- Q = 0
donc U = W
U = Cv ( Tf-To) avec Cv = nR/ - 1
Faire un bilan énergetique pour chaque partie est donner les expression de WB , WA, QA, QB, UA, UB en fonction de Cv et de To
En considérant le système R+A déduire la chaleur QR fournie par la résistance ?
Pour les deux derniers je ne comprend pas si vous pouvez m'aider svp
Merci d'avance
Bonjour
Tu commets plusieurs erreurs.
1° : A l'état final : l'immobilité du piston impose l'égalité des pressions de part et d'autre de celui-ci : PAf=PBf
2° : seul le gaz B subit une évolution adiabatique réversible. La loi de Laplace s'applique uniquement au gaz B.
3° : Ayant trouvé VBf par la loi de Laplace, tu peut obtenir VAf en remarquant que la somme des deux volumes est fixe.
4° : ensuite : équation d'état des gaz parfaits et premier principe...
Je te laisse réfléchir à tout cela et rectifier par toi-même...
Relis bien l'énoncé :
On chauffe lentement la partie A à l'aide d'une résistance chauffante
QA>0 !
Il faut bien une cause au mouvement du piston !
Quand le piston mobile se déplace vers la droite, le volume de B diminue, celui de A augmente. Tu vois bien sur le schéma que la somme des deux reste constante et égale à 2Vo.
Pour la partie B :
PAf = PBf = 5Po
VBf = ( (PoVo^ )/ PBf )1/
TBf = PBfVBf/ nR
Pour la partie A :
PAf = 5Po
VAf = 2Vo - VBf
TAf = 2PAf ( 2Vo - VBf ) / nR
c'est juste ?
OK pour tes calculs de volumes. Pour les températures : OK mais je pense qu'il faut au final remplacer nR par . Des simplifications apparaissent.
Pour la suite :
1° problème de notation : QA caractérise une quantité élémentaire de chaleur. Une quantité de chaleur se note QA
2° : le système global est délimité par une paroi fixe : W=0=WA + WB
Pour le système global :
U=QA puisque QB=0. QA représente la quantité de chaleur fournie par la résistance chauffante.
Tu as aussi : U = UA + UB
La première loi de Joule peut s'appliquer séparément à chaque gaz...
Ok donc pour le système global :
U = Q + W
or Q = QA + QB
QB = 0
Donc Q = QA = Cv ( TAf - To ) + nrTo ln VAf / Vo ?
Maintenant W = WA + WB
WA = -nRT0 ln VAF/ V0 et WB = Cv ( TBf - To )
donc W = -nrTo ln VAF/ V0 + Cv ( TBf - To )
Et pour conclure
L'energie interne pour le système global est :
dU = Cv(TAf-To ) + nrTo ln VAf/vo - nrTo ln VAf/V0 + Cv (TBf - To )
ce qui donne dU = Cv (TAf -T0 ) + Cv (TBf - To )
est ce que cela est juste ?
Tu n'as manifestement pas compris les notations en thermo : "d", "", ""... Il faut absolument te montrer rigoureux à ce sujet. Tu peux lire attentivement et bien comprendre les deux massages à ce sujet que tu trouveras ici : celui du 31-12-16 à 17:00 et les suivants :
mélange diphasée
Il n'existe pas de formule toute faite pour calculer une quantité de chaleur : tout dépend de la façon dont elle est fournie. La formule de QA que tu utilises est ici fausse. QA est la quantité de chaleur fournie par la résistance. Rien dans l'énoncé ne permet de la calculer directement. Je t'ai expliqué la méthode précédemment :
QA = U = UA + UB
Cet exercice est relativement subtil et demande de très bien connaître son cours... Est-ce le cas pour toi ? 
Tu fais ici un bilan entre un état initial et un état final. Tu n'as aucune variation élémentaire (dU...), aucune quantité élémentaire (Q, W...) à expliciter.
Comme déjà écrit : . As-tu bien compris pourquoi cette égalité est valide alors qu'écrire
serait faux ?
Première loi de Joule :
La capacité thermique molaire isochore Cvm peut s'exprimer en fonction de R et de ...
Annuler
connectez vous