Inscription / Connexion Nouveau Sujet
Thermodynamique
Bonsoir
S'il vous plait j'aimerais avoir de l'aide sur cet exercice.
On considère un fluide de masse volumique  , pouvant dependre éventuellement de la pression, en équilibre dans un champ de pesanteur terrestre uniforme g et occupant le demi espace z positif : la surface libre est le plan oxy et le demi -espace z négatif est a la pression uniforme
, pouvant dependre éventuellement de la pression, en équilibre dans un champ de pesanteur terrestre uniforme g et occupant le demi espace z positif : la surface libre est le plan oxy et le demi -espace z négatif est a la pression uniforme  0.
0.
1) le liquide est de l'eau supposer dans un premier temps, incompressible: déterminer la relation donnant l'expression de la pression en un point de profondeur z en fonction de p0,  , g et z
, g et z
Application numérique : déterminer la pression a une profondeur de 30m. P0=105la,  =103kg/m3, g=9.81m/s
=103kg/m3, g=9.81m/s
2) le liquide n'est plus supposé incompressible, mais caractérisé par son coefficient de compressibilité isotherme X=-1/V( V/
V/ p)T supposé continu. V représentant un volume quelconque de liquide
p)T supposé continu. V représentant un volume quelconque de liquide
Déterminer la masse volumique  en un point du liquide en fonction de la pression p en ce point, de la masse volumique
en un point du liquide en fonction de la pression p en ce point, de la masse volumique  0 du liquide sous la pression atmosphérique et de p0.
0 du liquide sous la pression atmosphérique et de p0.
3) en déduire l'expression de la pression en fonction de z.
Retrouver l'expression trouvée a la question 1) lorsque X tend vers 0.
Déterminer la pression a une profondeur de 30m si X=5.10-10 pa-1.  0=103kg/m3.
0=103kg/m3.
Conclure.
je suis bloqué a la troisième question. Les deux première m'ont donné
1) dP=- gdz
gdz
p-p0 =- gz car liquide incompressible et z0=0 .
gz car liquide incompressible et z0=0 .
2)  =Mp/RT donc
=Mp/RT donc
d =(M/RT)dp
=(M/RT)dp
Donc  =
= 0+(M/RT) (p-p0)
0+(M/RT) (p-p0)
3)- p=p0exp(-Mgz/RT)
La suite me dépasse. De l'aide s'il vous plait
Bonsoir
Étourderie je pense dans ta copie : il faut sans doute considérer le coefficient de compressibilité isotherme comme constant . En raisonnant sur le volume massique v de l'eau et en supposant la température T fixe :
A T fixe :
Par définition du volume massique :
Puisqu'il s'agit d'un liquide très peu compressible, les variations relatives de masse volumique sont très faibles. On peut éventuellement assimiler les différentielles à des variations :
L'intégration rigoureuse conduit à :
Un développement limité au premier ordre de l'exponentielle conduit au résultat précédent.
Tu devrais maintenant être capable de terminer seul...
Donc si j'ai bien compris
Pour avoir la pression, j'utilise l'équation de la statique des fluides
dP=- gdz et je remplace
gdz et je remplace  par sa valeur et je trouve
par sa valeur et je trouve
p=[p0(1+ 0Xgz) -
0Xgz) - 0Xgz] /(1+
0Xgz] /(1+ 0gXz) .
0gXz) .
Pour X=0,
P=p0- 0gz
0gz
C'est exact ?
Il faut partir de la relation fondamentale de la statique des fluides en considérant g indépendant de z :
Je te laisse résoudre cette équation différentielle...
J'ai utilisé un signe "+" car j'ai supposé l'axe (Oz) orienté suivant la verticale descendante puisque z semble désigner la profondeur. Dans ce cas : P est fonction croissante de z...
.
Le résultat me donne ce que j'ai fais dans mon message de 22h22.
Mais un sousi, pour X=0
On a éventuellement
p-p0= 0gz.
0gz.
merci vanoise
Le cas particulier 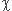 =0 doit effectivement conduire à l'expression simple correspondant au liquide incompressible. Revois la résolution d'une équation différentielle du premier ordre à coefficients constants. Le résultat que tu as fourni précédemment n'est pas homogène.
=0 doit effectivement conduire à l'expression simple correspondant au liquide incompressible. Revois la résolution d'une équation différentielle du premier ordre à coefficients constants. Le résultat que tu as fourni précédemment n'est pas homogène.
Bonjour vanoise
Quand je résous l'équation comme tu dis j'obtiens
P=-(1-Xp0)/X +[ (1-Xp0)/X +p0] exp( 0gXz)
0gXz)
Mais quand X tend vers 0 je n'obtiens pas l'expression de la première question. Ai je fais une erreur ?
Je n'ai pas vérifié ta solution de l'équation différentielle ...
Néanmoins, je ne suis pas d'accord avec ta remarque : "Mais quand X tend vers 0 je n'obtiens pas l'expression de la première question"
Si tu calcules la limite pour X tendant vers 0 dans l'expression que tu as trouvée de P ..., tu arrives à une indétermination du type 0/0
P=-(1-Xp0)/X +[ (1-Xp0)/X +p0] exp(0gXz)
P= (1-Xp0)/X) * (-1 + exp(rho0gXz)) + po.exp(rho0gXz)
lim(X-->0) [(1-Xp0)/X) * (-1 + exp(rho0gXz)) + po.exp(rho0gXz)] = lim(X-->0) [(1-Xp0)/X) * (-1 + exp(rho0gXz))] + po
Et lim(X-->0) [(1-Xp0)/X) * (-1 + exp(rho0gXz))] est une indétermination du type 0/0 qu'il faut lever.
Et par exemple, avec la règle du génial Marquis de Lhospital ;
lim(X-->0) [(1-Xp0)/X) * (-1 + exp(rho0gXz))] = lim(X-->0)[(rho0gz.exp(rho0gXz)-po.(-1 + exp(rho0gXz)))/1]
= lim(X-->0)[(rho0gz - po.(-1 + 1)/1] = rho0gz
Et donc lim(X-->0) [(1-Xp0)/X) * (-1 + exp(rho0gXz)) + po.exp(rho0gXz)] = rho0gz + po
... avec l'axe Oz dirigé vers le bas.
Sauf distraction. 
Je pars de l'équation différentielle donnée hier à 22h45. Pour alléger l'écriture, je pose u=P-Po. En remarquant : , elle peut s'écrire :
Solution particulière correspondant au cas : :
Solution de l'équation différentielle homogène (terme de droite nul) :
Solution générale :
Sachaant que u=0 en z=0, on obtient finalement :
Si la profondeur n'excède pas quelques centaines de mètres : ; cela autorise un développement limité de l'exponentielle. Je te rappelle le développement de exp(x) au voisinage de zéro, limité à l'ordre deux :
Je te laisse vérifier :
1° : l'expression obtenue est bien homogène ;
2° : le développement limité à l'ordre 1 conduit bien à l'expression obtenue en supposant le liquide incompressible ;
3° : le développement limité à l'ordre deux fait apparaaître un terme correctif lié à la compressibilité du liquide que tu vas devoir évaluer pour z=30m...
Remarque : cette étude à l'intérêt de montrer l'influence de la compressibilité du liquide mais elle n'est pas complète : il faudrait faire intervenir aussi sa dilatation en faisant intervenir le coefficient de dilatation isobare :
mais l'étude serait plus complexe car ce coefficient ne peut pas être considéré comme une constante, en particulier pour l'eau...
Une ligne de mon précédent message mérite d'être rectifiée :
si la profondeur n'excède pas quelques centaines de mètres : .
Bonsoir bissinyandoup
Je viens d'avoir la curiosité de développer l'expression de la pression que tu as fournie dans ton message du 07-04-18 à 09:02.
Après de nombreuses simplifications, on finit par obtenir l'expression que j'ai proposée. J'avoue ne pas être capable de reconstituer le cheminement qui t'a conduit à cette expression mais elle est correcte ...
Bonjour vanoise.
En après avoir trouvé la solution de l'équation homogène( que toi même tu as d'ailleurs calculer)
P=Aexp( 0gXz) , j'ai fais varié la constante A. Et j'ai dérivé P et remplacer dans l'équation général (avec second membre). Ce qui m'a permis de trouver cette constante
0gXz) , j'ai fais varié la constante A. Et j'ai dérivé P et remplacer dans l'équation général (avec second membre). Ce qui m'a permis de trouver cette constante


