Inscription / Connexion Nouveau Sujet
Thermochimie : Enthalpie standard de fusion
Bonjour,
Dans un exercice, j'ai la transformation 4/3 Al(s) + 02 (g) = 2/3 Al2O3 (g)
On effectue une transformation qui fait varier la température de 250K à 2300K tout en sachant qu'à 933K l'aluminium fond et que donc on a l'équation :
4/3 Al(l) + 02 (g) = 2/3 Al2O3 (g)
On doit calculer l'enthalpie standard de fusion.
Avec les données de l'énoncé et ce que j'ai trouvé, j'ai :
La variation d'entropie standard de 250K à 933K est : Delta G1 = -1116+0,208*T kJ.mol-1
La variation d'entropie standard de 933K à 2300K est : Delta G2 = -1130+0,224*T kJ.mol-1
On est dans les conditions d'approximation d'Ellingham.
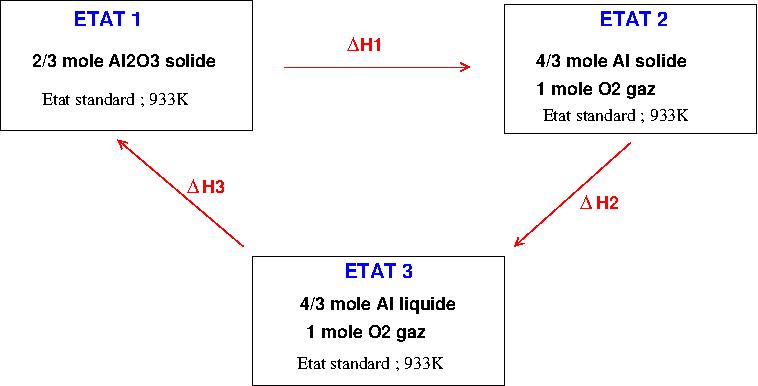
Ils demandent de faire un cycle thermodynamique pour trouver Delta H fusion mais je n'y arrive pas. J'ai tenté le cycle qui faisait Delta H2 + Delta H Fusion + Delta H3 mais je n'arrive pas à isoler Delta H Fusion car je n'ai pas la valeur totale de la somme.
Je vous remercie d'avance.
Bonjour,
La variation d'entropie standard de 250K à 933K est : Delta G1
Tu ne confonds pas par hasard entropie standard de réaction et enthalpie libre standard de réaction ???
Il n'est absolument pas nécessaire de "faire un cycle" !
Tu peux partir de l'expression générale de
 rG° en fonction de
rG° en fonction de  rH° et de
rH° et de  rS°.
rS°.
Que représente, dans l'approximation de Ellingham, la différence (1130-1116)kJ/mol ? Cela te donne directement le résultat !
A titre de vérification, tu peux aussi te demander ce que représente la différence (0,124-0,208)kJ/mol...
Si ce que je viens d'écrire ne te parait pas immédiatement évident, revois bien ton cours...
C'est la question qui demande de faire un cycle.
"A l'aide d'un cycle thermodynamique, déterminer DeltaFus H (Al), l'enthalpie standard de fusion de l'aluminium à 933K."
Sinon je me suis trompé en rédigeant, je voulais écrire "enthalpie libre standard de réaction" et non "entropie", je m'excuse.
Les valeurs que tu me demandes représentent la différence entre l'enthalpie standard liquide et l'enthalpie standard solide et pareil pour l'entropie (enfin je pense), mais pourquoi mettre une valeur absolue ? Je savais que je devais trouver un nombre positif mais j'ai fait en premier -1130 - (-1116) et on obtenait -14kJ au lieu de 14kJ qui serait cohérent avec la valeur réelle (11kJ)
Je n'avais pas fait attention : aux températures considérées, l'alumine est toujours solide et non gazeux.
Exprime  rH° et de
rH° et de  rS° en fonction des grandeurs molaires standard des constituants dans les deux cas.
rS° en fonction des grandeurs molaires standard des constituants dans les deux cas.
L'enthalpie molaire standard de fusion est la différence entre l'enthalpie molaire standard de l'aluminium liquide et l'enthalpie molaire standard de l'aluminium solide. Dans ces conditions, le résultat est évident ! Ton problème de signe va se résoudre tout seul !
Du coup, il n'y a pas besoin de faire de cycle ? Malgré la question ?
![]() (la question est partie B question B8)b)
(la question est partie B question B8)b)
D'après les données je trouve DeltaSm solide = -208 = 2/3 * 51 - 205 - 4/3 * 28
Delta Sm liquide = -224 = 2/3*51 - 205 - 4/3 * Sm° de l'Al liquide
Ce qui donne Sm° de l'Al liquide = 39,75
Du coup d'après votre aide, Entropie molaire standard de fusion = 39,75 - 28 =11,75
Et pour l'enthalpie cela donne : DeltaHm solide = -1116 = 2/3 * (-1674)
DeltaHm liquide = -1130 = 2/3 * (Hm liquide)
Donc Hm liquide = -1695
Et là d'après votre aide, enthalpie molaire standard de fusion = -1695 - (-1674) = -21. Mais ca a l'air faux donc je pense m'être trompé. Où ? 
Où chaque H° ou S° désigne la grandeur molaire standard du constituant précisé en indice.
La première méthode conduit à une enthalpie molaire standard de fusion de Al égale à 10,5kJ/mol ; la seconde méthode conduit à 11,2kJ/mol. L'écart de 6% peut s'expliquer par des arrondis dans les expressions fournies...
Je vous remercie pour votre réponse, l'expression écrite avec ce langage informatique est top, j'avais été confus par le fait que l'enthalpie standard de l'aluminium solide valait 0 et j'ai conclu directement que celle de l'aluminium liquide valait 0 aussi, à tort.
Ce n'est pas grave dans un concours si on trouve une réponse à une question sans suivre l'énoncé, en l'occurence sans faire le cycle thermodynamique ici ?
Ce n'est pas grave dans un concours si on trouve une réponse à une question sans suivre l'énoncé, en l'occurence sans faire le cycle thermodynamique ici ?
Tout dépend si la méthode est seulement suggérée ou au contraire, rendue obligatoire. Dans le premier cas, tu peux utiliser une méthode plus rapide si tu en connais une. Dans le second cas, il faut utiliser la méthode demandée.
La méthode du cycle est également très simple ; elle est seulement un peu plus longue à écrire et à dessiner (pour le cycle).
L'enthalpie étant une fonction d'état :
Pour l'homogénéité des formules, j'introduit un avancement
Tu peux éventuellement remplacer H par S...
Après division par
Juste une petite question, une grandeur de réaction étant par exemple X avec dX/d(avancement) la grandeur de réaction. Quand vous dites que H est une fonction d'état et non une grandeur de réaction c'est parce que l'on multiplie par l'avancement, je me trompe ?
Sinon ca reste une grandeur de réaction ?
Bonjour,
Soit X une fonction d'état extensive d'un système quelconque fermé susceptible d'évoluer par réaction chimique.
Relie bien mon message précédent : j'ai écris que , si H est une fonction d'état, l'enthalpie standard de réaction  rH° n'en est pas une !
rH° n'en est pas une !
De façon plus générale, une grandeur standard de réaction  rX°, pour une réaction donnée, ne dépend que de la température ; ce n'est donc pas une fonction d'état.
rX°, pour une réaction donnée, ne dépend que de la température ; ce n'est donc pas une fonction d'état.
En revanche, la grandeur de réaction  rX définie à partir des coefficients stchiométriques et des grandeurs molaires partielles dépend à la fois de P, de T et de l'avancement
rX définie à partir des coefficients stchiométriques et des grandeurs molaires partielles dépend à la fois de P, de T et de l'avancement : c'est une fonction d'état intensive du système.
Remarque : cette distinction entre grandeur de réaction et grandeur standard de réaction est extrêmement importante pour X = S et X = G comme tu l'as vu (ou le verra bientôt) dans l'étude des conditions d'équilibre chimique.
En revanche : pour X = H et X = U, la différence est faible et souvent négligée ; on pose souvent :  rH
rH
 rH° et
rH° et  rU
rU 
 rU°.
rU°.
Tu trouveras plus de détail à l'adresse suivante sur une fiche que j'ai rédigée il y a quelque temps :
![]()
Il s'agit de la fiche n° 6 de thermodynamique chimique, partie II.
Remarque : le fait d'introduire dans l'étude précédente est aussi une question d'homogénéité : on ne peut additionner des kJ et des kJ/mol !


