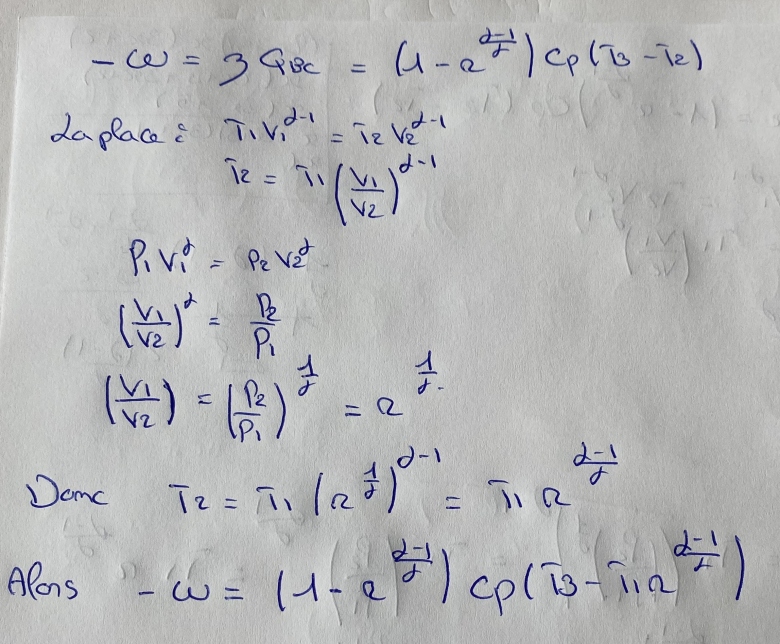Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Thermo - Moteur

Posté par
floflo03 17-03-22 à 16:48

Bonjour,

Bloquant sur un exercice type moteur à gaz.
Durant l'exercice, on me demande de trouver le rendement. Je trouve donc ceci : \eta =1-r^\frac{\gamma -1}{\gamma } , r=\frac{P2}{P1} P1= 0,7.10^5

A présent, on me demande quel est le taux de compression r qui donne le plus grand travail fournit par le cycle.

Je précise, c'est un moteur pour un avion d'une puissanc P à l'altitude 4000m.

J'ai donc pensé dans un premier temps à la formule du rendement : \eta =-\frac{W}{Qr}
Puis à dériver.
Mais je n'y arrive pas ... suis-je sur le bon chemin ?

Posté par
vanoisere : Thermo - Moteur 17-03-22 à 17:07

Tu es sûr de ton expression de r ? Cela devrait être une grandeur sans dimension, pas une pression !
Tu peux fournir l'énoncé intégral ? S'il est assez long, compte tenu de ce que tu as déjà écrit, tu peux fournir un lien du fichier au format pdf.

Posté par
floflo03re : Thermo - Moteur 17-03-22 à 17:17

vanoise @ 17-03-2022 à 17:07

Tu es sûr de ton expression de r ? Cela devrait être une grandeur sans dimension, pas une pression !
Tu peux fournir l'énoncé intégral ? S'il est assez long, compte tenu de ce que tu as déjà écrit, tu peux fournir un lien du fichier au format pdf.


Ma faute mauvaise rédaction r=P1/P2
Le P1 a coter est une valeur.

Posté par
vanoisere : Thermo - Moteur 17-03-22 à 17:30

Je comprends mieux malgré l'oubli de l'unité pour P1 mais sans l'énoncé intégral, impossible de fournir une aide efficace.

Posté par
floflo03re : Thermo - Moteur 17-03-22 à 17:54

vanoise @ 17-03-2022 à 17:30

Je comprends mieux malgré l'oubli de l'unité pour P1 mais sans l'énoncé intégral, impossible de fournir une aide efficace.


Je peux vous fournir l'énoncé :

Cycle de Brayton :
Compression adiabatique le gaz passe de (p1, V1, T1) à (p2, V2, T2).
Detente isobare (p2, V2, T2) à (p3, V3, T3).
Detente adiabatique (p3, V3, T3) à (p4, V4, T4).
Compression isobare (p4, V4, T4) à (p1, V1, T1).
Gaz parfait diatomique
M=28,8g.mol^-1
\gamma =\frac{7}{5}
Cv=\frac{5nR}{2}

Dans un premier temps, on représente le cycle de Brayton sur un diagramme de Clapeyron (p, V) et (T, S).
Puis on définit le rendement en fonction de T1, T2, T3 et T4.
On pose r=p2/p1 et on exprime le rendement en fonction de r et gamma.

Dernière question où je bloque :

On veut fabriquer un tel moteur pour un avion, ayant donc une puissance P à l'altitude 4000 mètres. On considère donc un cycle fonctionnant entre les températures T1 = 250K et T3 = 2400K, à la pression p=0,7.10^5 Pa. p1 et T1 sont la pression et la température extérieure. Lorsque l'air extérieur est admis dans le moteur, il a pour volume V1.

- Quel est le taux de compression r qui donne le plus grand travail fournit par le cycle ? Que vaut le rendement du moteur pour un tel taux de compression ? Comparez le au moteur de Carnot et concluez quant-à l'efficacité du moteur de Brayton.

Posté par
vanoisere : Thermo - Moteur 17-03-22 à 19:04

Sur un cycle :
|W|=|Q23+Q41|
Ce travail fourni sur un cycle s'exprime simplement en fonction de Cp,T1,T2,T3,T4 puis en fonction de Cp, T1, T3, r et .
Cp, T1 et T3 sont considérées, si je comprends bien, comme des constantes imposées et est aussi une constante. Tu obtiens ainsi |W| comme une fonction de r. Petit calcul de dérivée...

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 10:59

vanoise @ 17-03-2022 à 19:04

Sur un cycle :
|W|=|Q23+Q41|
Ce travail fourni sur un cycle s'exprime simplement en fonction de Cp,T1,T2,T3,T4 puis en fonction de Cp, T1, T3, r et .
Cp, T1 et T3 sont considérées, si je comprends bien, comme des constantes imposées et est aussi une constante. Tu obtiens ainsi |W| comme une fonction de r. Petit calcul de dérivée...


Personnellement je pense à : \eta =\frac{-W}{Q_{23}}
W=-\eta Q_{23}=(r^{\frac{\gamma -1}{\gamma }}-1)Cp(T_{3}-T_{2})
et si je ne fais pas d'erreur en dérivant par rapport à r
dW=(\frac{\gamma -1}{\gamma }r^{\frac{-1}{\gamma }})Cp(T_{3}-T_{2})


Qu'en pensez-vous ?

Posté par
vanoisere : Thermo - Moteur 18-03-22 à 11:48

Ce sont les températures T1 et T3 qui sont imposées. Tu peux donc partir de ton expression de W à condition d'exprimer T2 en fonction de T1, r et . Tu vas arriver au même résultat que celui que j'obtiens par la méthode que je t'ai indiquée. Ce n'est qu'ensuite qu'il faut dériver. Attention : on cherche à maximiser |W|, c'est à dire (-W).

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 11:55

**citation inutile supprimée**


D'accord je vois, j'essaye cela. Merci

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 12:33

**citation inutile supprimée**


Est-ce cohérent à votre avis ?

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 12:41

**citation inutile supprimée**


Thermo - Moteur

Attention : les recherches doivent être recopiées et non scannées!

Posté par
vanoisere : Thermo - Moteur 18-03-22 à 14:44

Je reprends tes calculs en détail. Je note d'entrée une incohérence : le rendement est une fonction croissante du taux de compression ”r” ; ce n'est pas ce que tu obtiens. Je reprends brièvement le raisonnement et les calculs.

Loi de Laplace sur les gaz parfaits :

T_{2}=T_{1}.r^{\frac{\gamma-1}{\gamma}}\quad;\quad T_{3}=T_{4}.r^{\frac{\gamma-1}{\gamma}}

Évolutions isobares :

Q_{23}=Cp.\left(T_{3}-T_{2}\right)\quad;\quad Q_{41}=Cp.\left(T_{4}-T_{1}\right)

Premier principe sur le cycle :

W+Q_{23}+Q_{41}=0

Rendement :

\eta=-\frac{W}{Q_{23}}=\frac{Q_{23}+Q_{41}}{Q_{23}}=1+\frac{Q_{41}}{Q_{23}}=1-\frac{T_{4}-T_{1}}{T_{3}-T_{2}} \\ \\ \eta=1-\frac{T_{4}-T_{1}}{T_{4}.r^{\frac{\gamma-1}{\gamma}}-T_{1}.r^{\frac{\gamma-1}{\gamma}}}=1-\frac{1}{r^{\frac{\gamma-1}{\gamma}}}=1-r^{\frac{1-\gamma}{\gamma}}

Travail fourni par cycle :

|W|=-W=\eta.Q_{23}=\eta.Cp.\left(T_{3}-T_{2}\right)

|W|=Cp.\left(1-\frac{1}{r^{\frac{\gamma-1}{\gamma}}}\right).\left(T_{3}-T_{1}.r^{\frac{\gamma-1}{\gamma}}\right) \\ \\ |W|=Cp.\left(T_{3}+T_{1}-T_{1}.r^{\frac{\gamma-1}{\gamma}}-\frac{T_{3}}{r^{\frac{\gamma-1}{\gamma}}}\right)

On peut poser :

f(r)=T_{3}+T_{1}-T_{1}.r^{\frac{\gamma-1}{\gamma}}-\frac{T_{3}}{r^{\frac{\gamma-1}{\gamma}}}

puis remplir un tableau de variations comme en maths pour montrer qu'il existe une valeur de r qui rend maximale le travail fourni par cycle.

Remarque : écrire directement :

|W|=Q_{23}+Q_{41}=Cp.\left(T_{3}-T_{2}+T_{1}-T_{4}\right)

puis remplacer T2 et T4 en fonction de T1,T3,r et  conduit au même résultat un peu plus rapidement.

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 15:02

**citation inutile supprimée**

D'accord merci pour votre aide, je vais reprendre ca demain à tête reposée.
Cependant
Q_{41}=Cp(T_{1}-T_{4}) au lieu de Q_{41}=Cp(T_{4}-T_{1})
En partant de \delta Q=CpdT ?

Posté par
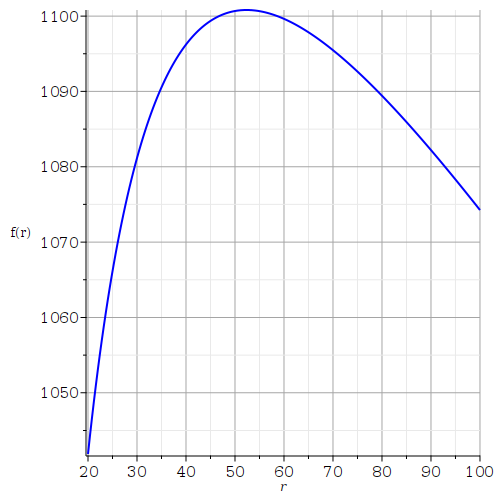
vanoisere : Thermo - Moteur 18-03-22 à 15:11

Effectivement : erreur d'indice sur Q41. Heureusement, il ne s'agit que d'une étourderie de copie qui n'a pas d'incidence fâcheuse sur la suite. Voici la courbe représentant les variations de f(r) en fonction de r. Bien sûr, tout cela est un peu théorique car industriellement, il est difficile d'obtenir des taux de compression aussi élevés.

Thermo - Moteur

Posté par
floflo03re : Thermo - Moteur 18-03-22 à 15:43

**citation inutile supprimée**


Ok génial merci pour l'aide en tout cas.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !