Mordus de thermodynamique, bonjour !!
Je planche sur mon DM, sans succès.. Voici l'énoncé:

On étudie la carabine du Père Noel.. Elle fonctionne de la manière suivante : un volume d'air de 5,0mL sous pression de 10 bars et à température initiale 50°C se détend rapidement sans le canon cylindrique de section 0,25 cm² et de longueur totale 100 cm (longueur comprenant l'air comprimé) en propulsant une balle de masse 1,0g dans l'atmosphère. On souhaite étudier la vitesse de la balle à la sortie du canon, ainsi que la température de l'air intérieur et sa pression à cet instant.

1_ Précisez clairement les hypothèses simplificatrices utilisées par ordre d'importance décroissante.
2_ Effectuez ensuite les calculs en utilisant le théorème de l'énergie cinétique pour la balle et les équations de la thermodynamique pour l'air comprimé. Pour l'air, on prendra C_p/C_v = 1,40
3_ Pourquoi a-t-on pris 50°C comme température initiale de l'air?


Je commence par traduire les données de l'énoncé:
longueur du canon L = 1 m
section du canon S = 0,25 cm² = 2,5.10^-5 m²
volume initial Vo = 5,0 mL = 5.10^-5 m³
pression initiale Po = 10 bars = 10⁶ Pa
température initiale To = 50°C = 323 K

Détente adiabatique, quasistatique d'un gaz considéré comme parfait (car Po est relativement faible). On a Q = 0, P.V = n.R.T, dU = n.C_vm.dT. La température donne que C_vm = 5R/2 donc C_pm = 7R/2

Les problèmes commencent là.. P, V et T varient pendant la détente, donc on ne peut pas appliquer les lois de Laplace, ni utiliser les coefficients de compressibilité 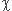, , . Il nous faut au moins 3 equations. On sait que Q = 0, donc dU = W, et on peut calculer n = Po.Vo/R.To = 1,86.10^-3 mol.

dW = -P.dV = n.R.T.(dV/V) mais comment intégrer ceci alors que T varie? (là, utiliser le coefficient = 1/V.dV/dT aurait été utile pour simplifier les choses)

dU = n.C_vm.dT

Comme dU = W, d²U = dW d'où n.R.T.dV/V = 5R/2.d²T, donc dV/V = 5/2.d²T/T

ok, mais je fais quoi avec ça? les variations de l'Ec de la balle ne me servent pas pour l'air lui même (je crois)..

Pour la troisième question, je pensais dire que quand la température augmente, la pression augmente de plus en plus difficilement, mais les forces augmentent fortement (l'Ec des molécules augmente). donc plus la température est élevée, moins l'air a besoin d'être comprimé pour fournir la même Ec à la balle.

Qu'en pensez-vous? Merci infiniment pour votre aide!