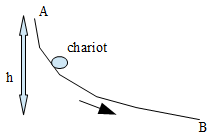
Voici un bien meilleur schéma de l'énoncé (je n'avais pas réussi à la mettre car elle était trop grosse)

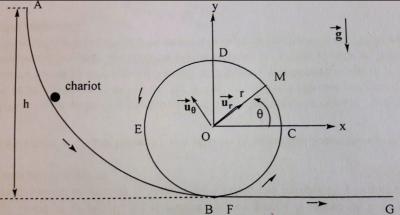
Bonsoir
De façon générale, le travail du poids est le produit de ce poids par la diminution d'altitude.
W=m.g.(zi-zf) avec
zi : altitude initiale
zf : altitude finale.
Je te laisse réfléchir à cela et proposer une solution.

J'ai utilisé l'expression de que j'avais trouvé et celle que j'ai trouvé avec ce que tu m'as dit ce qui donne :

et je trouve :
Est-ce que c'est juste s'il te plaît ?

Pour la deuxième question on nous dit :
Déterminer par la même méthode Vm la norme de la vitesse du chariot quand il se trouve au point M repéré sur le cercle par l'angle , en fonction de , h et des données. Vérifier que la formule permet de retrouver Vb.

J'ai fait le bilan des forces et je trouve la même chose que dans la première question puisqu'on nous dit que le chariot glisse sans frottement aussi sur ce cercle.

J'obtiens et comme pour la question 1. On a =mgr

Donc je trouve
Est-ce que c'est cela s'il-te-plaît ?

Attention: entre B et M l'altitude augmente,  le travail du poids est négatif. La formule que je t'ai indiquée s'applique et fournit bien une valeur négative. De B à M l'altitude augmente de
r+r.sin ()

Ok merci Donc si je comprends bien de B à C elle augmente de r puis de C à M elle augmente de ?
Du coup on a et je trouve . Est-ce que c'est ça s'il te plaît ?

Réfléchis au sens de ton calcul: selon lui: plus la masse monte plus elle va vite ! Irréaliste!
De B à M l'altitude augmente, le travail du poids est négatif!

Du coup je fais ?

Oui.
L'expression du travail du poids que je t'ai indiquée s'applique dans tous les cas de figures que W  soit positif ou négatif

Mais dans ce cas-là j'ai un problème, je ne peux pas passer à la racine pour trouver l'expression de Vm parce-que un des côtés de mon égalité est négatif

Attention à la masse m que tu oublies dans l'expression de l'énergie cinétique. Elle doit ensuite disparaître par simplification.
Ensuite il suffit de remplacer le carré de VB par sa valeur, d'isoler le carré de VM puis de prendre la racine carrée...

J'ai essayé de suivre ce que tu m'as dit et j'ai obtenu : Comment je fais pour passer à la racine ?

Puisque h est supérieur à 2r ton expression est positive et de plus correcte!

Ok merci

Et comment peut-on retrouver Vb à partir de cette expression puisqu'il n'apparaît plus ?

Tu es arrivée à :



Puisque : : ; puisque, selon le schéma : h>2r, on obtient bien :





Le cas particulier tel que M confondu avec B correspond à rad ; alors : ; on retrouve bien la valeur de V_B ! Tu pourrais aussi étudier le cas particulier du point D...

Ah ok merci je n'avais pas vu Je crois qu'on nous parle du point D dans une des questions qui suit
La question suivante est : Exprimer la norme de la réaction R(vecteur) exercée par le rail sur le chariot quand il est en M en fonction de , h et des données.

Voilà ce que j'ai fait (il y a des choses que je n'arrive pas à exprimer) :

D'après la 2e loi de Newton on a : vecteurP + vecteurR=m*vecteura
vecteurP=-mgr vecteur ur - mg(rsin)u

Là je ne suis pas sûr du tout de cette expression de P parce-que j'ai toujours du mal à trouver et comprendre comment exprimer les coordonnées d'un vecteur dans un repère cylindrique.

On a vm=
Là je pensais qu'on pouvait essayer de trouver l'accélération en dérivant cette expression mais finalement ça me paraît un peu compliqué....
Je pensais ensuite faire Rn-mgr=-m*vecteur a
mais du coup je ne sais pas comment trouver une autre expression de vecteura....

Tu dois connaître l'expression générale de l'accélération d'un point M en mouvement circulaire de rayon r : c'est la somme d'une accélération tangentielle et d'une accélération normale :


avec :


Dans le cas particulier du point D, sin()=1, valeur maximale possible ; la vitesse est donc minimale, sa dérivée par rapport au temps est nulle ; l'accélération tangentielle est nulle. L'accélération est donc uniquement l'accélération normale centripète : son vecteur est donc vertical descendant :
en D :


De plus, en D, les deux forces sont verticales orientées vers le bas, ce qui donne :


Je te laisse terminer le calcul et déterminer la norme R de la réaction de la piste.
J'imagine que la dernière question consiste à déterminer une condition pour que la masse m reste toujours en contact avec la piste... Il suffit d'écrire que la réaction R existe quelle que soit  la position du point M : cela suppose que la norme R reste constamment strictement positive...
Je te laisse réfléchir à tout cela et terminer seule le calcul...

J'ai bien lu toutes tes indications. Comme je trouve vecteur P  et vecteur R

D'après le bilan des forces et la seconde loi de Newton on a :
Donc en projetant sur on a :





Merci de me dire ce que tu en penses

Ok pour la projection mais erreur sur les 3 dernières lignes. Défaut d'homogénéité . Vérifie tes calculs.

Un peu plus de détail sur l'homogénéité : à une distance h, on ne peut ajouter un simple nombre comme tu le fais à la dernière ligne...

Jusque là tout va bien mais tu commets une erreur en développant ; je rectifie :



Tu peux vérifier l'homogénéité du résultat : R a bien la dimension d'une force...
Comme déjà expliqué, R est minimum quand sin() est maximum ; cela correspond au point D...