Inscription / Connexion Nouveau Sujet
Théorème de Millman
Bonjour, j'ai essayé à plusieurs reprise cet exercice mais je ne réussi pas.
Je dois exprimer la tension U en fonction de E, R et Rx en utilisant le théorème de Millman.
Qui dit que Vn(1/R1+....+1/Rn)=Va1/R1+......Van/Rn
Je trouve une réponse qui me semble fausse : Vn(1/Rx+3/R)=E/R et ensuite
Vn=E/R(1/Rx+3/R)
Merci
(je n'ai pas cadré la photo sur le schéma, l'énoncé est donc visible,j?espère que cela ne dérange pas)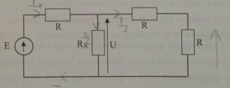
_______________
***Image recadrée => un énoncé doit être recopié***
Bonjour
Théorème de Millman en remarquant que les deux résistance « de droite » sont équivalentes à une résistance 2R :
Je te laisse simplifier. Pose des questions si tu ne comprends pas bien...
Je vois,merci
mais la résistance de gauche est équivalente aussi non ?, étant donné qu'elle font toutes les trois 1.5Kohm ?
mais la résistance de gauche est équivalente aussi non ?
Je ne comprends pas bien cette phrase...
La formule déduite du théorème de Millman prend bien en compte la résistance R en série avec E.
Si tu n'as pas bien compris le théorème de Millman, tu peux jeter un coup d'il à la fiche ci-dessous. Elle explique qu'il s'agit juste en fait d'une façon d'appliquer la loi des nuds en tenant compte de la loi d'Ohm...
ah super , donc pour les autres question ce sont de simple équations je vais les faire tu pourras me comfirmer ou non mes réponses ?
Raisonnement correct. On pourrait éventuellement discuter de la précision des résultats et du nombre de chiffres significatifs puisque l'énoncé pose R=1500 et non 1,5k
et non 1,5k ; il fournit ainsi 4 chiffres significatifs, même si cette précision me paraît un peu illusoire...
; il fournit ainsi 4 chiffres significatifs, même si cette précision me paraît un peu illusoire...
Dans ces conditions, il est préférable d'écrire pour Rx :
3000
1000
600,0
Je ne suis pas sûr que le concepteur de cet exercice accorde une grande importance à cette notion de chiffres significatifs...
oui, tu as raison, je ne penses pas également que les correcteurs accordent une grande importance mais c'est toujours mieux de faire le plus précis.
Et est ce qu'on peut regarder l'exercice d'après, car ça j'ai vraiment beaucoup de difficultés dessus.
Réseau 1 : tu peux regrouper les deux générateurs idéaux de tension en faisant bien attention aux orientations des dipôles.
Réseau 2 : remplacer le générateur linéaire de courant ( générateur de Norton) par le générateur linéaire de tension équivalent (générateur de Norton) puis regrouper les résistances. Attention là aussi aux orientations des dipôles.
Tu peux t'aider du schéma ci-dessous.
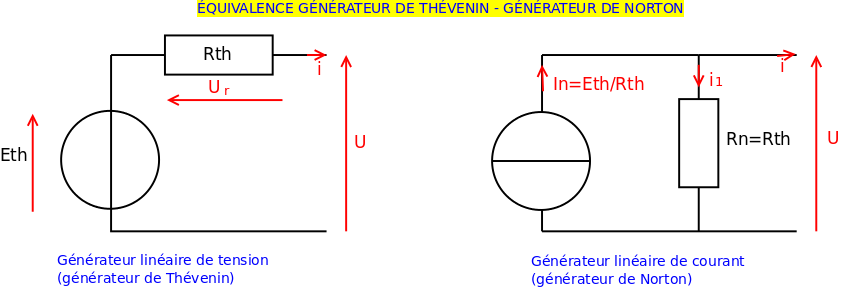
Réseau 1 : tu peux regrouper les deux générateurs idéaux de tension en faisant bien attention aux orientations des dipôles.
Réseau 2 : remplacer le générateur linéaire de courant ( générateur de Norton) par le générateur linéaire de tension équivalent (générateur de Norton) puis regrouper les résistances. Attention là aussi aux orientations des dipôles.
Tu peux t'aider du schéma ci-dessous.

une erreur non ?
Réseau 2 : remplacer le générateur linéaire de courant ( générateur de Norton) par le générateur linéaire de tension équivalent (générateur de THEVENIN)
Pour le réseau 2, je pense que ça devient comme le shéma ci dessus, on transforme en génératuer de Thevenin et la résistance est en série ?
Par contre le réseau 1, je ne vois pas
Un générateur idéal de tension de fém 6V en opposition avec un générateur de fém 3V, est équivalent à un générateur idéal de tension de fém 6-3=3V , orienté dans le sens de celui ayant la fém la plus élevée.
Désolé de ma réponse si tardive, donc je penses avoir réussi à dessiner les deux shémas et maintenant comment fait on pour calculer le générateur de thevenin ?
Pour le circuit 2 : Eth est le produit du courant contre électromoteur I par la valeur de la résistance montée en dérivation avec ce générateur idéal de courant. Si je lis bien les indices et les valeurs (photocopie un peu floue), cela donne :
Eth=R1.I=6 x 3=18V
R1 se retrouve ainsi en série avec R2 :
Rth=R1+R2=9
Pour le circuit 1 :
Rth=R=5
Eth=E2-E1=3V (attention à l'orientation)



