Inscription / Connexion Nouveau Sujet
théoréme de l'énergie cinétique
Bonjour, de laide svp
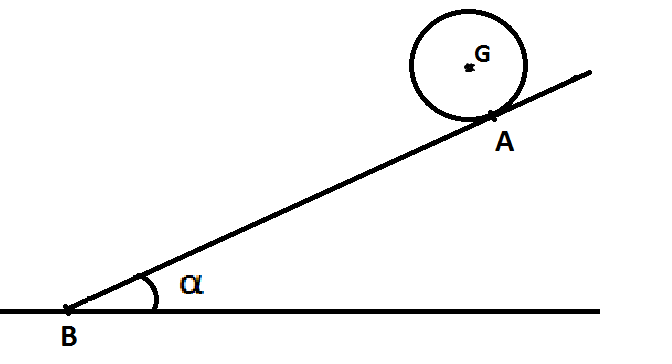
Un cylindre homogéne de masse m se déplace dans un plan incliné faisant un angle alpha avec l'horizontale.
Un mouvement de rotation : le cylindre tourne sur elle même
et un mouvement de translation : le solide part du point point A avec une vitesse initiale (Va) nulle et arrive au point b avec une vitesse Vb
il existe des forces de frottement de même direction que la pente et de sens opposés au déplacement de valeur constante F
Jo= 1/3 MR2
1)Exprimer le théoréme de l'énergie cinétique
merci d'avance
Bonsoir
Cet énoncé est surprenant au niveau première. La résolution rigoureuse demande l'utilisation des théorèmes de Koenig au programme des filières bac+2...
Pour résumer de façon simple :
L'énergie cinétique est la somme de deux termes :
L'énergie cinétique de translation dont tu connais l'expression en fonction de la masse et de la vitesse du centre d'inertie G ;
L'énergie cinétique de rotation qui s'exprime en fonction du moment d'inertie du solide par rapport à un axe horizontal passant par G et perpendiculaire au plan de figure et en fonction de la vitesse angulaire 
du solide .
La relation entre VG et s'obtient en considérant l'absence de glissement en A. L'existence du roulement sans glissement s'explique par l'existence d'une force de frottement comme expliqué dans l'énoncé.
Etourderie de copie sans doute : le moment d'inertie du cylindre homogène par rapport à son axe de symétrie auquel appartient le point G vaut :
JG = (1/2).M.R2
= 2W(P) + 2W(F) + 2W(R)Pourquoi multiplier par deux les travaux ?
Attention au piège : puisqu'il n'y a pas de glissement le long de la ligne de contact entre le cylindre et le plan incliné, la vitesse des points à la périphérie du cylindre s'annule à chaque fois que ces points sont en contact avec le plan incliné. Conséquence : les puissances des forces F et R exercées par le plan incliné sur le cylindre sont nulles à chaque instant . Ces deux forces ne travaillent pas. Seul le poids fournit du travail.
Comme déjà dit : avant d'appliquer le théorème de l'énergie cinétique, il faut exprimer l'énergie cinétique uniquement en fonction de la masse du cylindre et de la vitesse de son centre d'inertie. Cela suppose d'établir la relation entre VG et en tenant compte du roulement sans glissement.
Tu dois savoir que, dans le cas d'une force de vecteur F quelconque dont le point d'application se déplace à la vitesse V dans le repère d'étude, la puissance instantanée de la force a pour expression :
Donc : si ...
Mais tout cela : en classe de première ....
Annuler
connectez vous