Niveau licence

Température d'une pièce - Thermique

Posté par
cercus 06-02-19 à 15:59

Bonjour, ayant un exercice en thermique, j'aurais besoin de savoir si ma démarche est bonne. Voici l'énoncé :

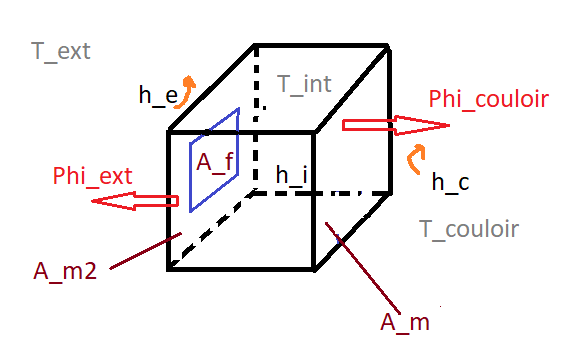
On considère une salle de classe ayant une fenêtre. En formulant des hypothèses convenables, trouver la température de la pièce après un (très) long cours magistral, sachant que l'on était 16 dans la pièce et qu'en moyenne, un être humain émet 100 W. On considère aussi 4 faces où les échanges de chaleur sont nulle. (Il y a des pièce avec la même température). le mur est constitué de 2 couches de plâtres et de l'air entre les 2. La fenêtre est un double vitrage. Ci-joint un schéma récapitulatif.

Ce que j'ai fais :

Hypothèse (trouvé avec l'aide de notre professeur) :
-> Régime permanent car le cours est supposé long
-> Pas de Soleil, de radiateur ou de ventilateur dans la pièce
-> T_p <T_int (T_p température de parois)
-> 4 faces adiabatiques

Source de chaleur : Puissance émis par les personnes dans la salle

Régime permanent donc P = $\Phi_{ext} + \Phi_{couloir} = 1600W$

Déterminons $\Phi_{couloir}$ :

-> Le mur étant constitué de 2 couches de plâtres d'épaisseur e₁ et de conductivité thermique _p . Entre les 2 couches, il y a une couche d'air de coefficient thermique h_air. On a donc $R_{th}^{m} = \frac{1}{A_m}(\frac{1}{h_i}+\frac{2*e_1}{\lambda_p} + \frac{1}{h_c} + \frac{2}{h_{air}})$

Donc $\Phi_{couloir} = \frac{T_{int}-T_{couloir}}{\frac{1}{A_m}(\frac{1}{h_i}+\frac{2*e_1}{\lambda_p} + \frac{1}{h_c} + \frac{2}{h_{air}})}$

Déterminons $\Phi_{ext}$ :

-> Le mur 2 est constitué d'une fenêtre double vitrage donc on a 2 couches de verre d'épaisseur e₂, de conductivité thermique _v et entre les 2 une couche d'argon d'épaisseur e₃ de conductivité thermique _argon.

Le mur et la fenêtre étant en "parallèle", on a $R_{th}^{m2} = \frac{1}{R_{th}^{f}} + \frac{1}{R_{th}^{mur2}}$

$R_{th}^{f} = \frac{1}{A_f}(\frac{1}{h_e}+\frac{2*e_2}{\lambda_v}+ \frac{e_3}{\lambda_{argon}} + \frac{1}{h_i})$ et $R_{th}^{mur2} = \frac{1}{A_{m2}}(\frac{1}{h_e}+\frac{2*e_1}{\lambda_p}+ \frac{2}{h_{air}} + \frac{1}{h_i})$

Donc $\Phi_{ext} = \frac{T_{ext}-T_{int}}{R_{th}^{m2}}$

On a donc $1600 = \frac{T_{int}-T_{couloir}}{R_{th}^{m}} + \frac{T_{ext}-T_{int}}{R_{th}^{m2}} <=> T_{int} = \frac{1600*R_{th}^{m}*R_{th}^{m2}+T_{couloir}*R_{th}^{m2}-T_{ext}*R_{th}^{m}}{R_{th}^{m2}-R_{th}^{m}}$

Bien cordialement,

$Température d\'une pièce - Thermique$

Posté par re : Température d'une pièce - Thermique 06-02-19 à 18:57

Bonsoir
D'accord avec tes calculs sur la résistance thermique de l'ensemble {mur2-fenêtre}.
Concernant le mur donnant sur le couloir : ton raisonnement conserve comme inconnue la température du couloir.
Le couloir possède-t-il un système de chauffage ? Si non, l'idée de conserver comme inconnue la température du couloir n'est pas très bonne. Personnellement, je calculerais la résistance thermique de l'ensemble série {mur+couloir+mur extérieur du couloir) puis j'écrirais que la résistance thermique de l'ensemble résulte de la mise en parallèle de cette résistance avec celle de l'ensemble {mur2-fenêtre}.
Sous toutes réserves...

Posté par re : Température d'une pièce - Thermique 06-02-19 à 19:08

La température du couloir est connue (on la mesure avec un thermomètre)

Posté par re : Température d'une pièce - Thermique 06-02-19 à 19:16

Dans ces conditions, ton raisonnement me parait correct !

Posté par re : Température d'une pièce - Thermique 06-02-19 à 19:20

Merci. J'avais juste un doute sur l'expression de $\Phi_{ext}$ (si c'etait (T_ext - T_int) ou (T_int-T_ext)

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Température d'une pièce - Thermique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique