Bonjour,

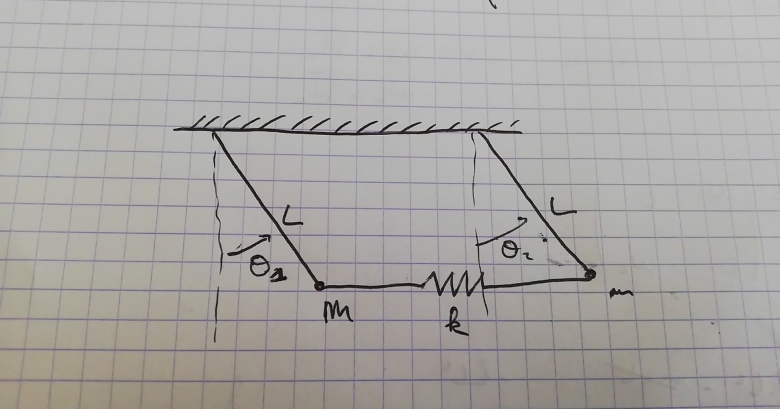
J'étudie le système constitué de deux pendules reliés par un ressort. A l'équilibre les tiges sont verticales. Par ailleurs les masses des tiges sont négligeables devant les masses m.

J'ai fait l'étude du système sans forçage en passant par les équations de Lagrange pour déterminer les équations du mouvement puis j'ai déterminé les matrices spectrale et modale.

Je dois maintenant étudié le système lorsqu'une force d'amplitude s'applique sur la masse de gauche et une force d'amplitude sur celle de droite. Ces forces sont horizontales et harmoniques de pulsation .

Dans sa correction mon professeur passe par le théorème des moments cinétiques pour retrouver les nouvelles équations du mouvement avec le terme de forçage.
Ayant utilisé les équations de Lagrange en première partie j'aimerai savoir s'il est possible de les réutiliser en rajoutant seulement le terme de forçage et si oui comment faire cela ?

J'aurais tendance a dire que le terme de forçage se rajoute dans le second membre de mes équations de Laplace et qu'il s'agit d'un moment de par la nature des termes précédemment obtenus. Mais il s'agit seulement de mon intuition et non d'une démonstration.

PS : Dites moi si vous souhaitez que je détaille l'obtention du système avec les équations de Lagrange.