Inscription / Connexion Nouveau Sujet
Systeme de prehension
Bonjours, étant en deuxième années de DUT je m'entraîne afin de passer le concours Ensea, par contre je rencontre pas mal de problème pour la meca.
Voila un exercice :pourriez vous me donner des pistes pour commencer s'il vous plait (il faut répondre vrai ou faux aux affirmations).
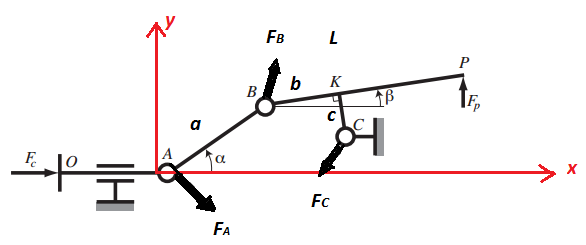
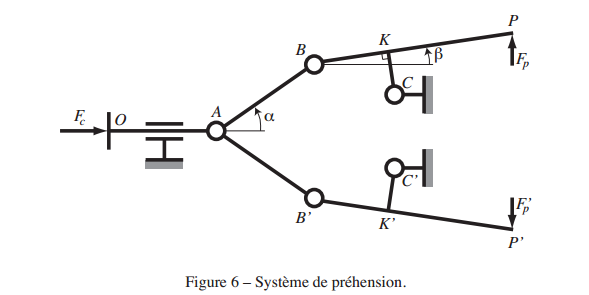
On s'intéresse au système de préhension schématisé sur la Figure 6, composé d'un bras OA, de deux mâchoires BP et B" P" et de deux biellettes AB et AB" disposées de manière symétrique par rapport à l'axe OA. Un effort de commande Fc est exercé sur l'entrée du système en O. Par symétrie, on pourra effectuer les calculs sur la partie supérieure uniquement. L'effort de commande est transformé en efforts de préhension Fp et F"p par le jeu des biellettes et des liaisons avec le bâti. On suppose dans cet exercice que toutes les liaisons sont parfaites, à l'exception du contact en P et P" entre les mâchoires et la pièce à tenir. Le système est paramétré de la manière suivante : AB = a, BK = b, BP = L, KC = c, . Par construction, l'angle
est un angle droit. L'étude du système se fait naturellement à l'équilibre
(A) Dans le cas général (β > 0), pour assurer l'équilibre de l'objet pincé en P et P" entre les deux mâchoires, il faut que le coefficient de frottement f entre chacune des mâchoires et l'objet considéré vérifie la relation suivante : f 
tanβ+tanβ = 2tanβ
(B) Si on étudie le système dans la configuration β = 0, le rapport d'amplification entre l'effort de commande et l'effort de préhension vaut :
(C) Le rapport d'amplification augmente si l'on augmente la longueur L des mâchoires.
(D) Le rapport d'amplification augmente si l'on augmente l'angle α.
(E) Le rapport d'amplification augmente si l'on augmente la longueur b.
Pour la A) je vois pas quoi faire
Pour la B) j'avais penser à la loi entré-sortie mais en fait je crois que ça à rien a voire.
Salut iizzii,
N'oublie pas mes bonnes pratiques de mécanique :
1. Définir le système => évident ici
2. Définir le référentiel => idem
3. Bilan des forces en présence => à faire
4. Schéma de la situation => à adapter au besoin : rajouter les paramètres de l'énoncé (longueurs, etc.)
Comme on l'a vu hier, dans un problème de dynamique, on peut écrire 3 équations :
1) Principe Fondamental de la dynamique en projection sur l'axe (je suppose que c'est l'axe horizontal) ;
2) Principe Fondamental de la dynamique en projection sur l'axe (je suppose que c'est l'axe vertical) ;
3) Equation du moment dynamique en un point judicieusement choisi, par rapport à (ers taxe dont la flèche point vers toi par rapport au plan
.
Ici c'est presque pareil, sauf qu'on suppose être à l'équilibre, donc le torseur dynamique est nul, ce qui revient finalement à faire une étude statique (PFS si tu connais l'abréviation 
).
_____
Forcément ici, tu as des liaisons, donc tu peux rajouter les efforts appliqués à chacune d'elles au niveau de leur point d'application.
Et te lancer dans toutes les équations possibles à écrire (pour les équations de moment, pense à utiliser les zéros des liaison, c'est-à-dire si tu appliques par exemple une équation de moment au centre d'une liaison pivot, eh bien ton équation n'aura pas dans sont expression les moments propres à ces liaisons (puisque qu'il y a rotation par rapport à )
Ok donc pour A), on sait que pour être à l'équilibre il faut que avec
angle d'adhérence, on sait aussi que
donc logiquement
Donc FAUX!
Ensuite :
Système : système de préhension.
Référentiel : terrestre supposé galiléen.
BAME: FC en O ; FP en P
Liaison : pivot : en A ; B ; C donc 1 degrés de liberté comme on est en 2D on aura une résultante en
Donc PFS : 
Alors pour la première question :
A. Pourquoi faux ? Le principe d'une pince est bien à ce que tu agrippes l'objet en question, et qu'il y ait donc de l'adhérence. A partir de f = tan 
de chaque côté, il y glissement.
Pour la suite, il est où mon schéma avec tous les efforts représentés (y compris les actions des liaisons) ?
Ok j'ai compris pour A) en fait j'ai mal lu le cours en fait si f = tan il y a équilibre stricte donc ça marche, et si f > tan il y à adhérence donc les deux marches. Donc VRAI.
Salut iizii,
Comment tu as trouvé ton résultat ?
Tjs détailler ses résultats 
Au passage, bonne année à toi !
Alors,
je ne vais malheureusement ne pas avoir bcp de temps,
malgré tout, je te conseille décomposer les efforts aux liaisons pivots en une composante X (selon l'axe Ox) et une composante Y selon l'axe Oy.
Alors
Si on reprend ton schéma :
PFS par rapport à Ox :
PFS par rapport à Oy :
donc
ce qui fait bcp d'inconnues ...
Il faut donc avoir un nombre suffisant d'équations pour résoudre ce pb.
Tu peux pour cela déterminer le degré d'hyperstatisme du système pour savoir combien d'équations de moments il faut.
Eq Mt en B par rapport à Oz :
et ainsi de suite :
Eq Mt en C / Oz
Eq Mt en A / Oz
Parce que dans ton calcul, tu oublies que l'énoncé te dit qu'on étudie la configuration
et je ne vois pas comment du te retrouves directement sans les inconnues de liaison.
Heu je vais essayer, mais cela me semble bizarre, car tout transporter prend énormément de temps (concours en temps limité), et ensuite on aura que 5 équations, 2 des résultantes, et 3 des moments alors qu'il y a 6 inconnus...
Mais merci quand meme, deja je trouve pareil que toi pou le moment en B
Effectivement,
Je t'ai donné la méthode générale, il doit y avoir plus simple :
j'ai trouvé ceci :
Qu'en penses-tu ?
Annuler
connectez vous