Inscription / Connexion Nouveau Sujet
Système de charges
**Bonjour**
dîtes mois si j'ai tort quelque part, mais ne me donnez pas de solutions, s'il vous plaît..
toutes les sphères ont la même masse, et sont toutes sur une surface lisse, non conductrice.
les deux sphères chargées portent une charge +q.
on coupe la corde en haut, trouvez la vitesse maximum des deux sphères d'en bas.
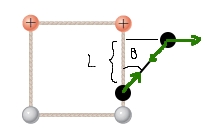
j'ai pensé à fixer un référentiel à la sphère 4, on aura alors 2 qui bougera en cercle.
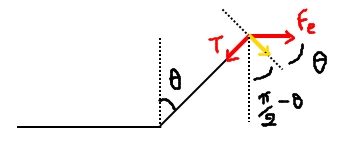
par symétrie, la force électrique sera toujours horizontale, et la seule à travailler.
on trouvera alors la vitesse depuis l'énergie cinétique, et on la multipliera par , pour obtenir sa composante verticale, puis on la divisera par deux, et on maximisera le terme variable sous la racine carrée.
on divise par deux car 2 et 4 commencent avec une vitesse initiale nulle, et ont la même composante de force verticale (mais sont de signes opposés), et qu'on a fixé la référentiel en 4.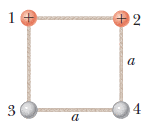
Bonjour cafeLatte et bienvenue sur l'
merci de prendre connaissance de 
[***A LIRE AVANT D'AGIR***] Règles du forum
et de
extrait de 
la FAQ du forum :Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
guide latex
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le 
mode d'emploi du forum(pour les formules, l'éditeur Ltx est fortement conseillé)
avec une première aide ici :
[lien]
mais aussi
extrait de la FAQ du forum :Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?
équivalences des systèmes de niveaux scolairesdonc commence par renseigner ton profil avec ton niveau, afin que l'aide soit la plus adaptée possible.
Bonsoir
Le système composé des quatre billes est pseudo isolé. Son centre d'inertie reste donc fixe et confondu avec le centre de gravité du carré initial. Un repère ayant ce point pour origine et ayant des axes de directions fixes est donc galiléen, ce qui n'est pas le cas de celui que tu as choisi. On peut aussi trouver des symétries dans ce problème. Tu pourrais faire un schéma soigné d'une situation intermédiaire et la poster ici.
Peux-tu recopier l'intégralité de l'énoncé ?
Bonsoir
Le système composé des quatre billes est pseudo isolé. Son centre d'inertie reste donc fixe et confondu avec le centre de gravité du carré initial. Un repère ayant ce point pour origine et ayant des axes de directions fixes est donc galiléen, ce qui n'est pas le cas de celui que tu as choisi. On peut aussi trouver des symétries dans ce problème. Tu pourrais faire un schéma soigné d'une situation intermédiaire et la poster ici.
Peux-tu recopier l'intégralité de l'énoncé ?
466/5000
Quatre petites sphères de masse égale m, deux avec une charge + q et deux non chargées sont reliées par des chaînes légères et non conductrices de longueur a, comme indiqué sur la figure. L'ensemble est ensuite placé sur une surface horizontale, lisse, non conductrice et la corde entre les deux sphères chargées est coupée. Déterminez la vitesse maximale des deux sphères non chargées après la coupe de la corde.
Annuler
connectez vous